[arXiv:2409.04057v1] Self-Harmonized Chain of Thought

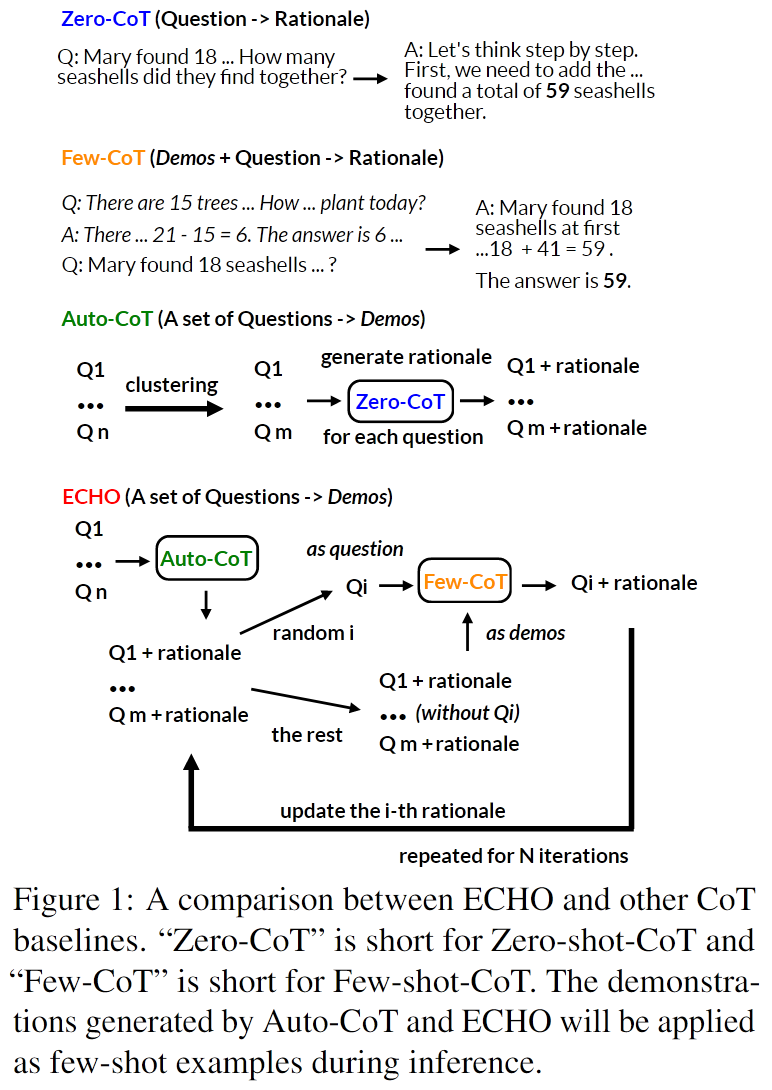
ECHO 与 常见 CoT 方法对比

这里 Demos 就是 prompt 里要给的示例. motivation 是 Few Shot 过程给的示例多样性可能不够好, 通过自优化 demos 来提升 prompt 质量. 也可以用到 Zero Shot, 将数据集分为指定数量demonstrations, 每个demonstrations 取一个典型问题, 解典型问题的 rationale (也就是思维链) 作为 demos.

具体的优化过程是, 先用 Auto-CoT 方法生成典型问题的 Demos, 然后以一个典型问题作为真正的问题, 其余典型问题作为 Demos, 从而逐个优化问题的思维链, 得到高质量的 Demos.

[ICLR2025 Poster] Don’t Take Things Out of Context: Attention Intervention for Enhancing Chain-of-Thought Reasoning in Large Language Models

和 ACL2023 Towards understanding chain-of-thought prompting: An empirical study of what matters 研究内容相似的, 研究 CoT Dimensions. 代码未开源, 图画的清晰但比较烂

Motivation: Few-Shot CoT 中, 示例可能会干扰 LLM 的生成过程, 引入噪声. 比如示例里说某人有160个罐子, 当输入问题与罐子有关时, 输出答案很可能受到影响. 可视化 Attention 也可以看到, 有一部分 Dimensions token 与其他 token 的关系不大, 但是这些 token 依然保留了自身的语义熵信息, 在某些时间步上显著影响输出

Contribution:

  1. 揭示了 Dimension Tokens 影响输出的问题
  2. 提出 Few-Shot Attention Intervention(FAI), 动态分析 Dimensions 的 attention matrix, 识别具有孤立语义的 token, 修改注意力层权重阻断这些 token 对输出 token 的影响

Case Analysis

论文使用显著性技术 (Saliency techniques, 2013) 来分析模型内部的信息流动, 综合考虑注意力分数和梯度, 分析 tokens 间信息流动. 既有研究用模型最终输出计算显著性分数, 但 CoT 在模型生成过程中也会有影响, 所以作者动态分析了 LLMs 里的信息流动

显著性分数矩阵如下, 其中 ⊙\odot 代表 Hadamard product(矩阵对应点乘), Ah,l,tA_{h, l, t} 代表第 tt 个时间步在第 ll 层的第 hh 个头的 attention weight, xtx_t 是第 tt 个时间步预测的 token. 某个 token 在第 ll 层生成时的显著性分数即 attention weight 与损失函数对 attention weight 的微分两个矩阵对应点乘, 所有头求和

Sl,t=∣∑h(Ah,l,t)⊙∂L(xt)∂Ah,l,t∣ S_{l,t} =\left | \sum_h (A_{h, l, t})\odot \frac{\partial \mathcal{L}(x_t)}{\partial A_{h, l, t}} \right|

上述变量可以衡量在时间步 tt, 第 ll 层的第 jj 个 token 到第 ii 个 token 的信息流动量

实例

以上是生成 next token 时的实例: 当前生成 token 与 160 对应的 token 的显著性分数大 (图例颜色更深), 此时受该 token 影响生成了 “160”, 但正确的 token 对应的文本是 “8”. 还是很符合直觉的

在 GSM8K 上实验, 构建了一个模型答案受到 dimensions 影响导致错误的数据集, 数据集内的错误类型分为 4 类:

  1. Few-Shot 示例中引入错误 (IF)
  2. 数学计算错误 (MC)
  3. 推理步骤中的错误 (RS)
  4. 重复输出错误 (RO)

IF, MC, RS 样本基本都受到 dimensions 的影响, RO 样本则没有, 进一步证明了以上论点. 但是这里只取了一共 180 个样本分析, 数据量不大.

Few-Shot Attention Intervention(FAI)

FAI 分析需要干预的 token 位置, 然后下一层中干预, 这里应该是操作的 mask. 上面的显著性分析需要 loss 反向传播, 计算开销太大了, 所以实际计算 token 间信息流时使用注意力分数构建聚合系数 α\alpha 来衡量信息聚合程度

具体而言, 给定一个具有 LL 层的 LLM, 每层包含 H 个注意力头, 对于 dimensions 中的每个 token tit_i, 我们首先计算其在第 l 层所有注意力头中的平均注意力分数:

A‾l=∑h=0HAlhH\overline{\mathcal{A}}_l = \frac{\sum_{h=0}^H\mathcal{A}_l^h}{H}

这里 Alh\mathcal{A}_l^h 是 attention weight matrix, 上面 A‾l\overline{\mathcal{A}}_l 其实就是把每一层所有头的 attention weight matrix 加权取平均. 然后取 αlti=A‾(ti,ti)\alpha_l^{t_i} = \overline{\mathcal{A}}(t_i, t_i) 作为 token tit_i 在 ll 层对自己的 attention score. 可以这样取是因为 attention matrix Alh\mathcal{A}_l^h 是归一化的, 对自己的注意力分数高代表对其他 token 的注意力分数小, 所以 $\alpha_l^{t_i} $ 高代表这个 token 在输入中的语义信息相对孤立, 信息聚合

设置阈值 τ=λindexxi\tau = \frac{\lambda}{index_{x_i}}, α\alpha 高于阈值时认为 token tit_i 信息孤立. 这里 λ\lambda 是超参数, indexxiindex_{x_i} 是在 demo 中 token 索引

除以 index 没懂, 原文 “其中 indexti 表示 token ti 在其所属 demonstration 中的索引。鉴于注意力矩阵 Ah l 已经归一化，若注意力分数在同一 demonstration 内均匀分布，则项 1 / indexti 近似等于指向 token ti 的注意力分数的均值”

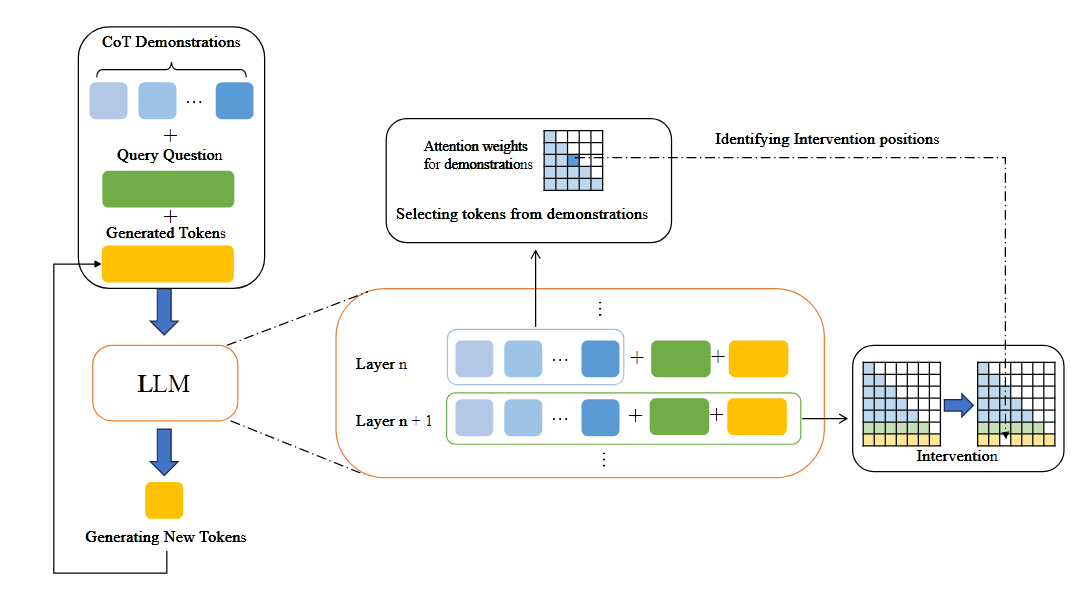
Few-Shot Attention Intervention(FAI)

识别到需要干预的 token 位置后, 修改 attention mask, 实现对 token 生成的干预. 实验结果显示大概有 15%-30%的 demontion token 被干预了, 还是很多的. 简单有效的方法

[EMNLP2024] Nash CoT: Multi-Path Inference with Preference Equilibrium

Motivation 来自 DPO, 但是使用纳什均衡作为选择答案的标准, 而不是优化 LLM 参数. 改进的问题是 self consistency 中多路径推理缺乏确定最优推理路径数量的理论基础, 需要增加路径数来保证性能, 计算消耗大

纳什均衡: 假设每个参与者都知道其他参与者的均衡策略, 那么没有任何参与者可以通过改变自己的策略而获益

作者定义偏好均衡为 reward model 对策略 A 优于 B, 和 B 优于 A 两种状态收益的纳什均衡. 当达到偏好均衡时, 角色沉浸 LLM 生成的偏好与无模板 LLM 生成的偏好一致, 且显然后者多样化更好. 因此偏好均衡可以衡量 LLM 生成多样化和准确率的关系

Nash CoT 对每个问题的推理分为 Answer Gathering 和 Answer Filtering 两个阶段.

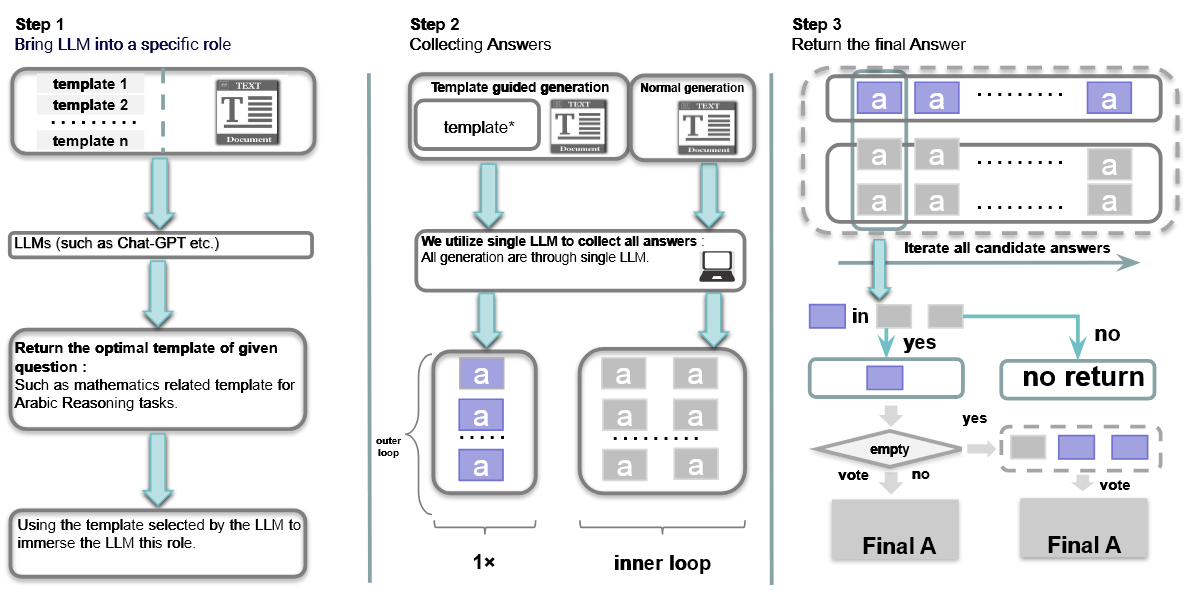
  1. Answer Gathering: 小批量循环. 然后进行两次外层循环, 也即 noutern_{\text{outer}} 次小批量循环. 最终保留最频繁达到偏好均衡的答案作为预测答案

  2. Step 1: 预设上有很多种 prompt template, 根据问题自适应选择 noutern_{\text{outer}} 种 template

  3. 用上面的 prompt template 和正常 prompt 生成两组答案, 正常 prompt 采样 ninnern_{\text{inner}} 次答案为第二组. 此时进行了 nouter+ninnern_{\text{outer}} + n_{\text{inner}} 次生成

  4. 利用以上生成, 得到符合偏好均衡的答案

Nash-CoT

[ACL2024] Adaption-of-Thought: Learning Question Difficulty Improves Large Language Models for Reasoning

现有 prompting 方法没有区分问题的难度, 对简单问题存在 overthinking 现象, 对困难问题无法引入足够的知识来回答. 因此, 作者提出了 Adaption-of-Thought (ADOT). 评估问题难度, 根据难度构造 demos.

  1. 衡量问题难度. 难度由语法复杂度和语义复杂度决定, 前者由句子长度决定, 后者由回答与问题中的非重复语义词数量来决定. 所有问题被离散的分为了三种难度.
  2. 自适应构建一个 demos 集合. 这里作者引入变异系数 v∈[0,1]v\in[0, 1] 来题目难度的分布程度, 值越高代表难度分布越分散, 即有更多简单和困难的题目. 取 p=v2p=\frac{v}{2} 为简单题目和困难题目的比例, 剩下为普通题目

    v=n∑i=1ndi×1n∑i=1n(di−d‾2)v = \frac{n}{\sum_{i=1}^n d_i}\times \sqrt{\frac{1}{n}\sum_{i=1}^n(d_i-\overline{d}^2)}

  3. 自适应抽取 demos. 简单题目使用原始 few-shot demos; 普通题目进行了指代消解操作, 减少歧义; 困难问题进行指代消解和增加推理步骤间的详细联系, 增加联系这一步是将样本问题与目标问题难度差异最小的 demos 作为目标问题的 demos

ADOT

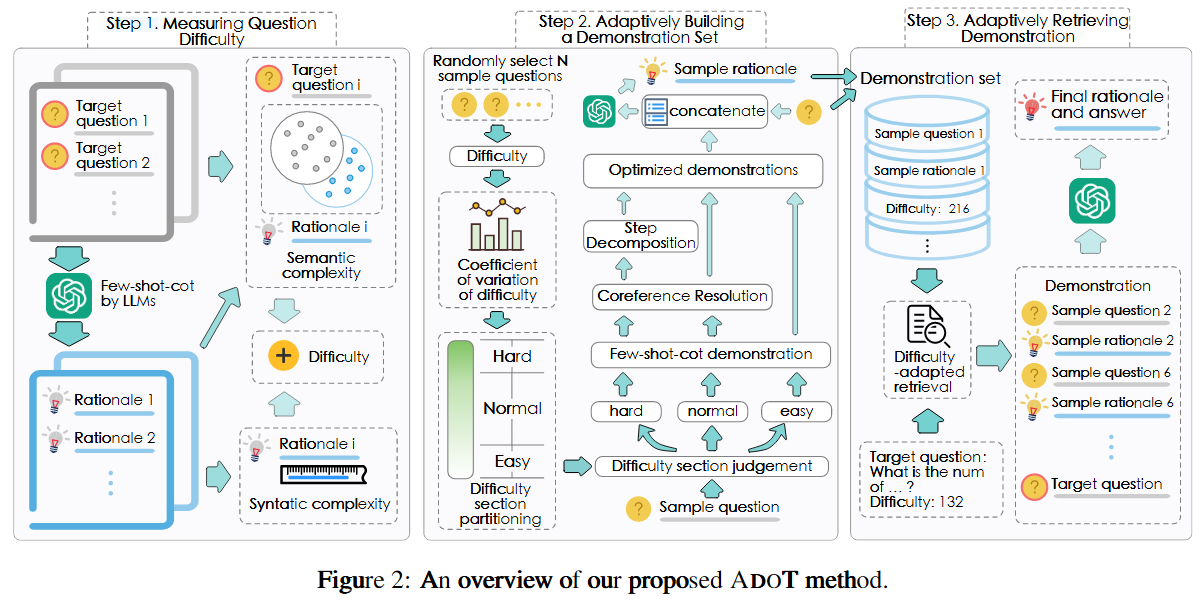
如果把问题难度改成连续的衡量方式应该会更好

[ICLR2024 poster] Boosting of Thoughts: Trial-and-Error Problem Solving with Large Language Models

迭代多个 trees-of-thoughts, boosting 实现

BoT

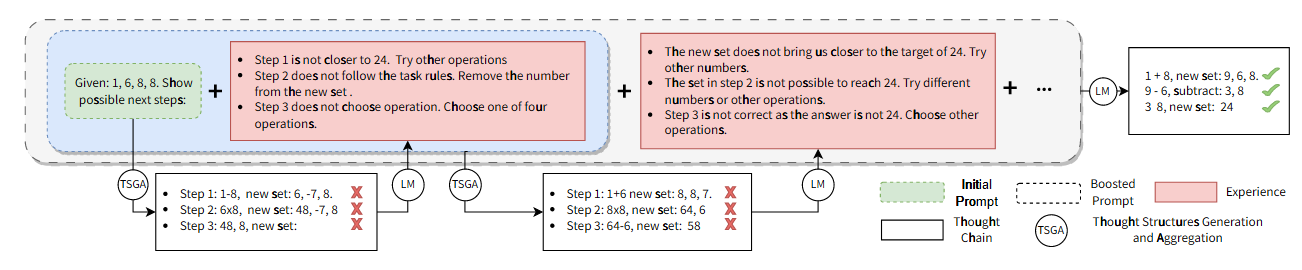
[ICML2024 poster] Toward Adaptive Reasoning in Large Language Models with Thought Rollback

用 LLM 分析思维链中错误链的索引, 然后从该位置的前一个时间步重新生成, 达到回溯的效果

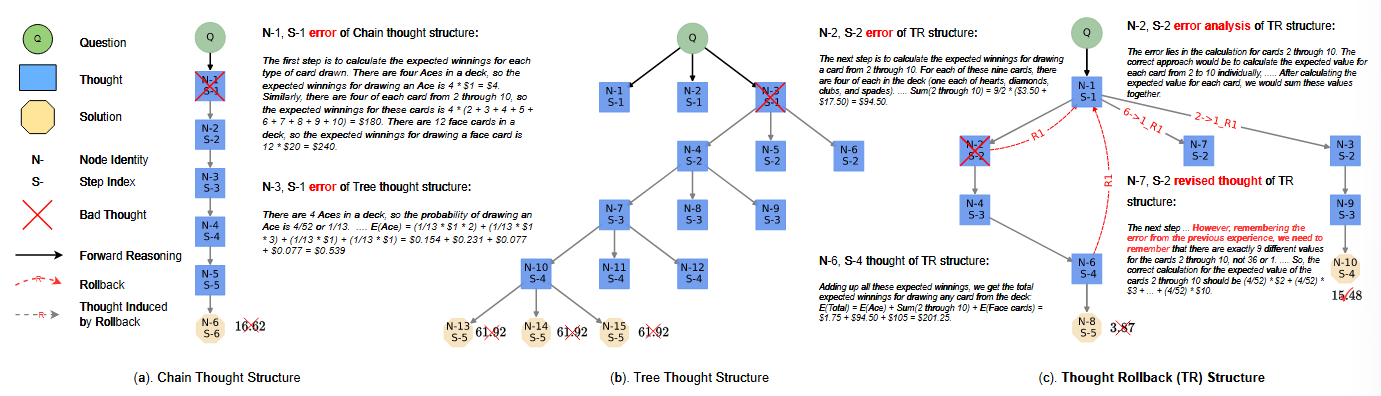
CoT+Thought Rollback(TR)

和 BoT 是同一个作者, 同一个代码框架, 加新数据集都很困难 :(. 看上去回溯的方法很直接有效, 但是回溯后是通过 prmopt enhancer 来增强推理的, 这样的话不如直接最开始就使用增强后的 prompt? 代价上比没增强的应该没多多少, 还可能要更少.

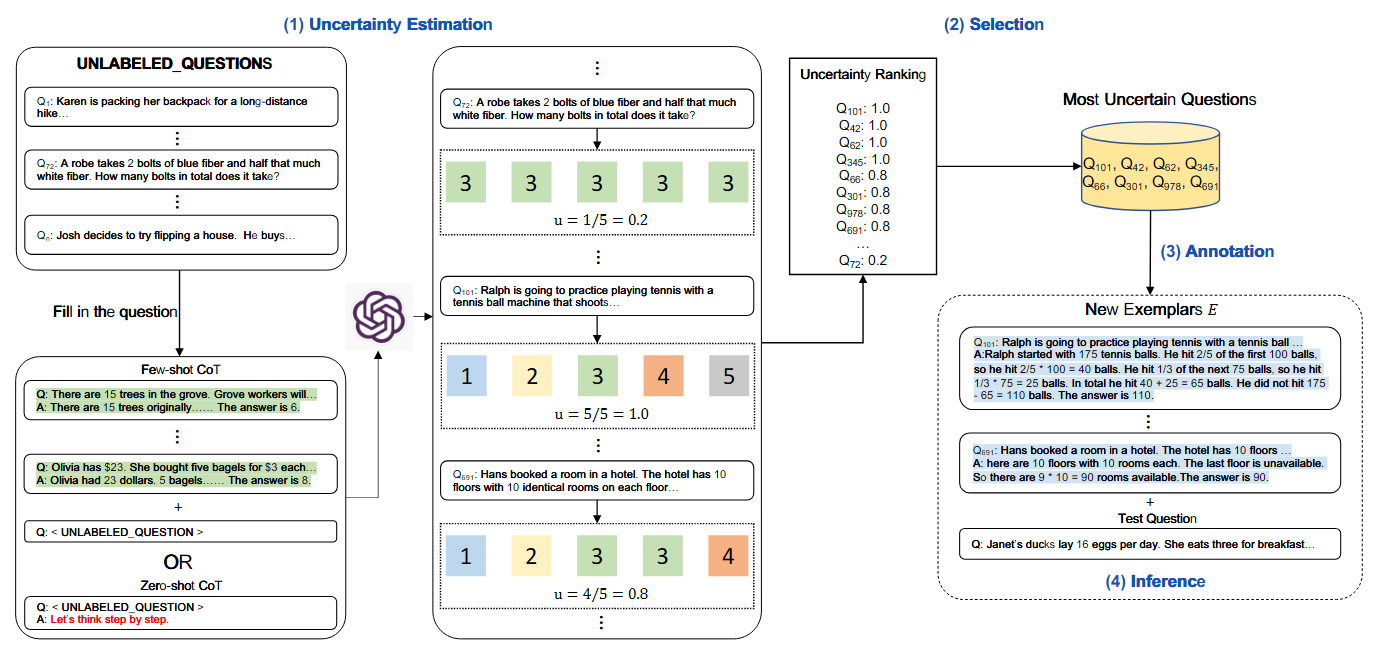
[ACL2024] Active Prompting with Chain-of-Thought for Large Language Models

将 unlabeled question 多次回答后计算 disagreement 或熵, 手动回答不确定性最高的问题, 将其作为 demos. 原始到不像是2024的工作

Active Prompting