Calculation-Logits

[ACL2024 Long Paper] Shifting Attention to Relevance: Towards the Predictive Uncertainty Quantification of Free-Form Large Language Models

Motivation

与 prompt 相关的 token 在不确定性估计中是否比不相关的 token 更为关键?

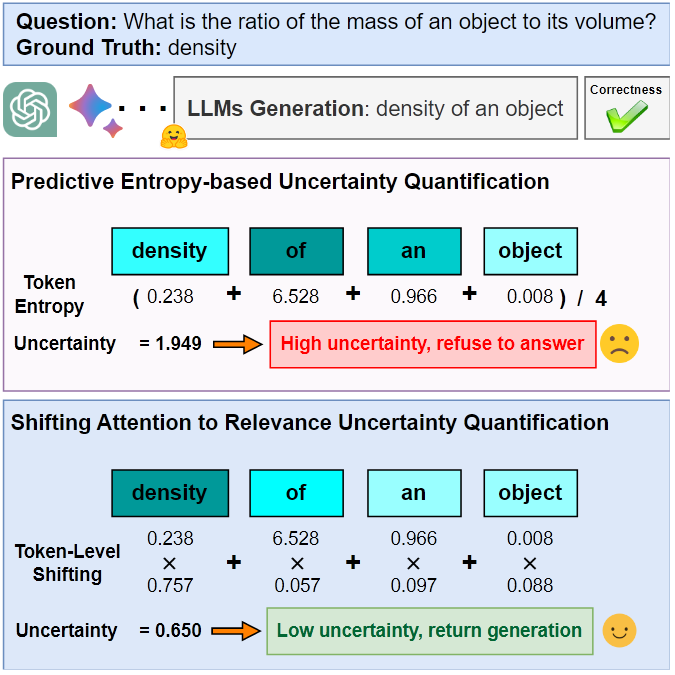
论文以 Predictive Entropy 为 Baseline, 通过引入 Relevance 和 Uncertainty Proportion 来回答上面的问题. 前者用来衡量 token 或句子语义相关度, 越高代表语义越重要; 后者用来衡量 token 或句子的不确定性, 越高代表承载的不确定性价值越高

Predictive Entropy 的计算公式为

$PE(\boldsymbol{s}, \boldsymbol{x}) = -\log p(\boldsymbol{s}|\boldsymbol{x}) = -\sum_{i}\log p(z_i|\boldsymbol{s}_{<i}, \boldsymbol{x})$

在 token 级别, 有

$\begin{aligned} R_T(z_i, \boldsymbol{s}, \boldsymbol{x}) &= 1-|g(\boldsymbol{x}\cup\boldsymbol{s}, \boldsymbol{x}\cup\boldsymbol{s}\backslash \{z_i \})|\\ UP_T(z_i, \boldsymbol{s}, \boldsymbol{x}) &= \frac{-\log p(z_i|\boldsymbol{s}_{<i}, \boldsymbol{x})}{PE(\boldsymbol{s}, \boldsymbol{x})} \end{aligned}$

公式里的 “\” 代表集合的差集

这里 $\mathbf{x}$ 代表输入的 prompt, $z_i$ 代表第 $i$ 个 token, $\boldsymbol{s}$ 代表句子, $\mathbf{x}$ 代表输入, $g(\cdot, \cdot)$ 计算两个句子的相似度, 具体而言论文使用 Cross-Encoder-RoBERTa-large 方法

在 sentence 级别, 有

$\begin{aligned} R_S(\boldsymbol{s}, S, \boldsymbol{x}) &= \sum_{j=1, j\neq i} g(\boldsymbol{s}_i, \boldsymbol{j})p(\boldsymbol{s}_j|\boldsymbol{x})\\ UP_S(\boldsymbol{s}, S, \boldsymbol{x}) &= \frac{PE(\boldsymbol{s}_i, \boldsymbol{x})}{\sum_k PE(\boldsymbol{s}_k, \boldsymbol{x})} \end{aligned}$

这里 $S$ 代表包括所有句子的集合, $\boldsymbol{s}$ 代表句子, $p(\boldsymbol{s}_j|\boldsymbol{x})$ 代表句子 $\boldsymbol{s}_j$ 的概率, $1\leq k\leq K$, $1\leq i,j\leq K$

直观上看, token-level 的 Relevance 反映了 token $z_i$ 在句子 $\boldsymbol{s}$ 中的语义重要性, 计算了去除该 token 前后句子语义的变化幅度, 再用 1 减去上值; Uncertainty Proportion 反映了 token $z_i$ 承载的不确定性价值, 计算了 token $z_i$ 的朴素熵占整个句子不确定性的比例. sentence-level 同理

依次计算每个 token 或句子的 Relevance 和 Uncertainty Proportion, 得到如下结果: 仅有少量 token 具有较大的 Relevance 和 Uncertainty Proportion; Relevance 越小, Uncertainty Proportion 越大, 说明承载语义信息少的 token 承载的不确定性价值更高 (某种二次证明, 符合直觉)

Conclusion: 与 prompt 相关的 token 在不确定性估计中比不相关的 token 更为关键, 应当给予更高的权值

Method

token-level

Shifting Attention to Relevance (SAR). 定义句子 $\boldsymbol{s}_j = \{z_1, z_2, \dots, z_{N_j} \}$, $N_j$ 表示句子 $\boldsymbol{s}_j$ 的长度. 基于 Motivation 部分的公式, 将句子内部不同 token 的 Relevance 进行归一化. 包含 $N_j$ 个 token 的句子 $\boldsymbol{s}_j$ 的 Relevance 为

$\tilde{R}_T(z_i, \boldsymbol{s}_j, \boldsymbol{x}) = \frac{R_T(z_i, \boldsymbol{s}_j, \boldsymbol{x})}{\sum_{n}^{N_j} R_T(z_n, \boldsymbol{s}_j, \boldsymbol{x})}$

然后向语义重要的 token 增加权值, 修改句子的 Predictive Entropy 计算公式为

$E_T(z_i, \boldsymbol{s}_j, \boldsymbol{x}) = -\log p(z_i|\boldsymbol{s}_{<i}, \boldsymbol{x})\tilde{R}_T(z_i, \boldsymbol{s}_j, \boldsymbol{x})$

于是得到整个段落进行 token 语义偏移后的熵为

$\mathrm{TOKEN}\mathit{SAR}(\boldsymbol{s}_j, \boldsymbol{x}) = \sum_{i}^{N_j} E_T(z_i, \boldsymbol{s}_j, \boldsymbol{x})$

sentence-level

语义上一致的句子比其他句子更具说服力, 所以可以通过提高语义一致的句子的生成概率来减少句子的不确定性

$\begin{aligned} E_S(\boldsymbol{s}_j, S, \boldsymbol{x}) &= -\log \left( p(\boldsymbol{s}_j|\boldsymbol{x}) + \frac{1}{t}R_S(\boldsymbol{s}_j, S, \boldsymbol{x})\right)\\ &= -\log \left(p(\boldsymbol{s}_j|\boldsymbol{x}) + \underbrace{\frac{\sum_{k\neq j}g(\boldsymbol{s}_j, \boldsymbol{s}_k)p(\boldsymbol{s}_k|\boldsymbol{x})}{t}}_{\text{sentence relevance}}\right) \end{aligned}$

这里 $p(\boldsymbol{s}_j|\boldsymbol{x}) = \prod_i p(z_i|\boldsymbol{<i}, \boldsymbol{x}$ 是句子 $\boldsymbol{s}_j$ 的生成概率, $t$ 控制偏移幅度的温度系数 (代码里默认是 0.001). 于是得到整个段落进行 sentence 语义偏移后的熵为 ($K$ 为段落中的句子数)

sentence-level 进行偏移的方法比较粗糙. 计算单个句子的熵时, 作者在句子出现的概率上加了一个有关于 Relevance 的项, 通过这一项的温度系数来控制偏移幅度
为什么这个温度系数可以控制偏移幅度呢? 这里公式是熵的形式, 真数 (也就是对数函数的自变量处) 进行线性增长, 线性增长的系数控制函数的增长速度. 在该语境下, (对单一句子而言的) 语义一致的句子的 Relevance 本身更大, 从而乘系数后得到的增幅更大, 进而与语义不一致的句子的熵的差值更大 (感觉说的有点糊涂了, 下面的例子更直接吧)
类比, 2*10=20 和 4*10=40, 虽然乘数相同, 但是结果差距变得更大了, 从而增加了真数部分的差值, 进而提高了语义一致句子的熵与语义不一致句子的熵的差值

$\mathrm{SENT}\mathit{SAR}(S, \boldsymbol{x}) = \frac{1}{K}\sum_k E_S(\boldsymbol{s}_k, S, \boldsymbol{x})$

值得注意的是, sentence-level 计算单一句子的熵形式与语义熵相似, 本文作者提出语义熵 (ICLR2023) 在平均超过 20 个 token 的长句中表现不理想, 而本方法会更好. orz, 平均超过 20 个token, 这个长度有点长了?

语义熵的计算公式如下

$\begin{aligned} SE(x) &= -\sum_c p(c|x)\log p(c|x)\\ &= -\sum_c \left(\left(\sum_{\mathbf{s}\in c} p(\mathbf{s}|x)\right) \log\left[\sum_{\mathbf{s}\in c} p(\mathbf{s}|x)\right] \right) \end{aligned}$

主要区别在于, 负对数概率乘的权值不同, 语义熵是直接乘以句子的生成概率, 而本文是乘以句子的 Relevance

Overall Measurement

token-level 和 sentence-level 的两种偏移处理方法各有不同, 但他们是正交的, 可以自然地结合起来. 为此, 只需将 sentence-level 方法的每个句子的生成概率替换成 token-level 方法的偏移概率即可. 也即

$\begin{aligned} p'(\boldsymbol{s}_i|\boldsymbol{x}) &= e^{-\mathrm{TOKEN}\mathit{SAR}(\boldsymbol{s}_i, \boldsymbol{x})}\\ p'(\boldsymbol{s}_j|\boldsymbol{x}) &= e^{-\mathrm{TOKEN}\mathit{SAR}(\boldsymbol{s}_j, \boldsymbol{x})}\\ E_{T,S}(\boldsymbol{s}_j, S, \boldsymbol{x}) &= -\log (p'(\boldsymbol{s}_i|\boldsymbol{x}) + \frac{\sum_{k\neq j}g(\boldsymbol{s}_j, \boldsymbol{k})p'(\boldsymbol{s}_j|\boldsymbol{x})}{t} \end{aligned}$

因此, $K$ 个句子的 token- and sentence-level shifted predictive entropy 为

$\mathit{SAR} = \frac{1}{K}\sum_k E_{T, S}(\boldsymbol{s}_k, S, \boldsymbol{x})$

附录关于温度系数 $t$ 的消融实验表明, 使用 $t=1\times10^{-3}$ 和 $t=1\times10^0$ 区别不大. 感觉这个 sentence-level 的偏移方法还是粗糙了一些, 可以优化.

[ICLR2024 Workshop] How Many Opinions Does Your LLM Have? Improving Uncertainty Estimation in NLG

语义熵使用多项式采样, 多项式采样会倾向于生成多个序列的相似样本, 这在计算上是低效的, 且一些语义类可能被忽略. 基于此, 论文提出 SDLG (Semantic Diverse Language Generation), 搜索那些具有高概率且具有高语义多样性的输出序列. 论文代码未开源

具体而言, 文章提出计算 Attribution score, Substitution score, Importance score. Attribution score 根据推理的梯度, 确定哪个输出序列中的 token 应该被更改; 该分数表示当 token $y_i$ 被更改时, 对语义的影响越大. Substitution score 表示用词表的哪个 token 替换更好; 该分数越高表示 Embedding 的变化与语义变化更一致. Importance score 表示在给定上下文情况下, 用替代 token 替换当前 token 的可能性; 该分数越高表示替换当前 token 时的可能性越大/重要性越高.

计算完所有替代 token $v_i$ 的三个分数后, 根据分数对潜在替代项排序, 然后用排名最高的替代 token 替换既有生成 token, 然后按原有解码方式 (一般式多项式采样) 继续生成过程.

Calculation-Internal State

[ICML2024 Poster] Characterizing Truthfulness in Large Language Model Generations with Local Intrinsic Dimension

过去一些文章研究了神经网络的内在维度 Intrinsic Dimension, 本篇文章基于过去的一些工作在 LLM 的 Local Intrinsic Dimension (LID) 上进一步研究

Problem Setup

考虑 Casual LLM $M$, 含有 $N$ 个 token 的输入序列 $X = [x_1, x_2, \dots, x_N]$, 含有 $O$ 个 token 的输出序列 $M(X) = [x_{N+1}, x_{N+2}, \dots, x_{N+O}]$. 这里输出 token $x_{N+i}, i\in[1, \dots, O]$ 等价为在前缀 $x_1, x_2, \dots, x_N, x_{N+1}, \dots, x_{N+i-1}$ 下从模型词表 $\mathcal{V}$ 中采样的结果

$\mathbf{X} = (M_L \circ M_{L-1} \circ \cdots \circ M_0)(x_1, dots, x_{N+i-1})\\ p(x_{N+i}|[x_1, \dots, x_{N+i-1}]) = \mathrm{softmax}(W\mathbf{X}_{Li}+b)$

这里 $M_j, j\in [1, \dots, L]$ 是 LLM 的第 $j$ 层, $M_0$ 是 Embedding 层, $W$ 和 $b$ 是输出层的权重和偏置, $\mathbf{X}_{Li}$ 是第 $j$ 层的输出, 后续用 $\mathbf{X}_{ji}$ 表示第 $j$ 层 Embedding 输出的第 $i$ 个 token $x_{N+i}$ (是一个 $D$ 维向量), $p(x_{N+i}|\cdot)$ 表示单一 token $x_{N+i}$ 的分布, 同理 $p(M(X))$ 表示 $M(X)$ 的分布.

考虑有 $n$ 个样本的数据集 $\mathcal{D} = \left\{X^1, \dots, X^n\right\}$, 我们想得到一一对应的数据集可信度集合 $\left\{M(X^1), \dots, M(X^n)\right\}$. 这里使用 $\left\{\hat{Y}^1, \dots, \hat{Y}^n \right\}$ 表示真实值, 使用 $s\left(M(X^i), \hat{Y}^i \in \{0, 1\} \right)$ 作为输出是否可信的指示函数.

以往工作大多从预测分布 $p(M(X)|\cdot)$ 中获取特征, 本文从中间表示 $\mathbf{X}_{ji}$ 的 LID 中进行探索

MLE Estimator for LID

酸爽的前置知识学习环节

MLE estimator for LIDs 是2004年的工作, 用于估计单个 point(点) 的 local instrisic dimension (LID, 局部内在维度), 这与其他 global 估计的方法不同

以下的讨论中, 我们选定模型中间某一层的最后一个 token, 从而在讨论中忽略 layer 和 token 的下标

对于数据集 $\mathcal{D}$ 中的一个数据点 $\mathbf{X}^i$, MLE 估计器将泊松过程拟合到其近邻点的数量上. 形式上, 考虑数据点 $\mathbf{X}^i$ 的 $T$ 个最近邻点 $\{\mathbf{X}^{i1}, \dots, \mathbf{X}^{iT}\}$; 考虑 $\mathbf{X}^i$ 为中心, 半径为 $R$ 的一个球 $S_{\mathbf{X}^i}(R)$; 在半径 $0<t<R$ 的球内近邻点数量可以表示为以下二项过程

$N(t, \mathbf{X}^i) = \sum_{k=1}^T\mathbb{I}\{\mathbf{X}^{ik}\in S_{\mathbf{X}^i}(t) \}$

上述过程可以用速率为 $\lambda(t)$ 的泊松过程来近似, 假设密度 $f$ 在点 $\mathbf{X}^i$ 附近近似恒定, 并且体积 $V$ 与 $t^m$ 成比例扩大 $V = V_mt^m$, 这里 $m$ 是内在维度的数量. 于是有

$\lambda(t) = f\frac{\mathrm{d}V}{\mathrm{d}t} = fV_mt^{m-1}$

泊松过程涉及到随机过程这门课, 放弃之

所以泊松过程的对数似然可以写成内在维度数 $m$ 和 $\theta = \log f$ 的函数

$L(m, \theta) = \int_0^R\log \lambda(t)\mathrm{d}(N_{\lambda}(t)) - \int_0^R\lambda(t)\mathrm{d}t$

最大化上述对数似然函数, 得到计算内在维度 $m$ 的公式

$m(R, \mathbf{X}^i) = \left(\frac{1}{N(R, \mathbf{X}^i)} \sum_{j=1}^{N(R, \mathbf{X}^i)} \log\frac{R}{Q_j} \right)^{-1}$

这里 $Q_j, j=1, \dots, T$ 是中心点 $\mathbf{X}^i$ 与第 $j$ 个近邻点 $\mathbf{X}^{ij}$ 之间的距离. 上式可以进一步简化为

$m(\mathbf{X}^i) = \left(\frac{1}{T-1} \sum_{j=1}^{T-1} \log\frac{Q_T}{Q_j} \right)^{-1}$

并未手动推导上述公式,

Layer Selection and Distance-aware MLE

在上一节, 讨论了如何计算 $\mathbf{X}^i$ 的 LIDs. 在大模型中计算的话, 存在两个问题

1. 每一层的表示维度为 $D$, 所以很难说用哪个是最优的
2. MLE 假定密度函数 $f$ 是恒定的, 这在 Causal LLMs 不成立

解决方法有两种

Layer Selection

LLMs 在每层为每个 token 生成一个 $D$ 维的表示. 这里选择 $\mathbf{X}^i$ 的最后一个 token 即 $\mathbf{X}^i_{-1}$ 作为这一层的表示

但是实验证明, 最后一层 layer 的表示可能不是最具信息量的特征 (LIDs 预测真实性的性能与测试集上 LIDs 绝对值的总和有很好的相关性, 但在某些层上有所偏移). 这里建议选择 $l$ 层

$l = \argmax_l\sum_{i=1}^n m\left(\mathbf{X}_{l\{-1\}}^i \right) + 1$

Distance-aware MLE

为了缓解泊松过程做最大似然估计时的密度不均匀问题, 可以调整泊松过程的速率 $\lambda(t)$. 既有研究指出, 可以用 $\hat{\lambda}(t) = fV_mmt^{m-1} + t^mV_m\delta(t)$ 替代 $\lambda(t) = fV_mmt^{m-1}$, 这里 $\delta(R)$ 是受 $\mathbf{X}^i$ 几何性质限制的修正函数, 其具体形式参加原论文 (雾)

有了新的速率, 可以重新进行最大似然估计, 对结果进行泰勒展开, 再使用多项式回归计算修正, 然后然后

卒. 评价是不是我现在能快速看懂的论文

[ICLR2025 Poster] Improving Uncertainty Estimation through Semantically Diverse Language Generation

与语义熵类似, 多次采样生成 M 个句子; 然后用另一个模型将所有自然语言映射至 Embedding, 计算 Embedding 间的余弦相似度, 用以计算 Semantic Embedding Uncertainty (SEU), 这里 $\mathrm{cos}(\mathbf{e}_i, \mathbf{e}_j) = \frac{\mathbf{e}_i\cdot \mathbf{e}_j}{|\mathbf{e}_i | |\mathbf{e}_j |} $

$\mathrm{SEU}(x) = 1-\frac{2}{M(M-1)} \sum_{i=1}^{M-1}\sum_{j=i+1}^{M} \mathrm{cos}(\mathbf{e}_i, \mathbf{e}_j)$

语义熵在语义聚类时是离散聚类的, 一个回答只能属于一个语义类, 这种余弦相似度实现了连续空间内的语义统计

实验设置: 论文采样设置 5 次, 温度系数 0.5 (ICLR2023 SE 的工作也是 0.5). 生成答案与参考答案的 Rouge-L 分数大于 0.3 视为正确, 评估方法是 AUROC, 没有和 Nature2024 的工作比较, 和 ICLR2023 的工作比较了. 代码未开源, OpenReview 还没提交最终版本

Blackbox

[ICML2024 Oral] Decomposing Uncertainty for Large Language Models through Input Clarification Ensembling

一句话概括: 本文聚焦于偶然性不确定性, 提出了一种和 Deep Emsemble 对称的不确定性度量方式, 通过对输入进行"澄清", 从而减少输入的偶然不确定性. Whitebox 和 Blackbox 均可以使用

Uncertainty Decomposition 是将预测模型的不确定性分解为偶然不确定性(数据不确定性)和认知不确定性(模型不确定性), 前者是数据生成汇总固有的随机性引起的, 后者是模型训练数据缺失引起的. 既有的 UD 研究主要研究偶然不确定性

$\boldsymbol{X}$ 和 $\boldsymbol{Y}$ 代表任务的输出输出, $\theta$ 代表 LLM 的参数; $p(\boldsymbol{Y}|\boldsymbol{X})$ 和 $q(\boldsymbol{Y}|\boldsymbol{X}, \boldsymbol{\theta}$ 分别代表真实分布和模型分布. 总不确定性 total uncertainty 是预测分布的熵 $\mathcal{U} = \mathcal{H}(q(\boldsymbol{Y}|\boldsymbol{X; \boldsymbol{\theta}}))$, 由偶然不确定性 aleatoric uncertainty $\mathcal{U}_D$ 和 认知不确定性 epistemic uncertainty $\mathcal{U}_E$ 组成

贝叶斯神经网络 Bayesian Neural Network(2015) 和深度集成 Deep Ensembles(2017)

贝叶斯神经网络 (BNN) 对神经网络的参数分布进行建模, 给定训练数据, 可以通过变分推断近似后验分布. 这种方法计算成本很高;

深度集成有更好的扩展性, 维护 K 个模型, 每个模型的参数为 $\boldsymbol{\theta}^{(k)}$, 最小化每个模型训练的损失函数, 相当于完成优化问题 $\min \mathrm{KL}(p(\boldsymbol{Y}|\boldsymbol{X})\|q(\boldsymbol{Y}|\boldsymbol{X}, \boldsymbol{\theta})).$, 不同模型的初始值不同, 优化后的参数也不同, 所有模型的参数可看成采样结果, 根据采样结果估计参数的分布 $p(\boldsymbol{\theta}|\mathcal{D})$, 这里 $\mathcal{D}$ 是训练数据集. 所以贝叶斯网络的集成分布可以表示为 $q(\boldsymbol{Y}|\boldsymbol{X}) = \mathbb{E}_{q(\boldsymbol{\theta}|\mathcal{D})} [q(\boldsymbol{Y}|\boldsymbol{X}, \boldsymbol{\theta})].$, 所以不确定量可以表示为

\mathcal{H}(q(\boldsymbol{Y}|\boldsymbol{X}) = \underbrace{\mathcal{I}(\boldsymbol{Y}; \boldsymbol{\theta}|\boldsymbol{X})}_{\textcircled1} + \underbrace{\mathbb{E}_{q(\boldsymbol{\theta}|\mathcal{D})} [\mathcal{H}(q(\boldsymbol{Y}|\boldsymbol{X}, \boldsymbol{\theta}))]}_{\textcircled2}

这里 $\mathcal{L}$ 是在 $q$ 分布下的互信息. 第一项用于衡量不同模型见的分歧, 第二项用来衡量单独模型的平均不确定性, 两项可以近似于认知不确定性和偶然不确定性

上述两种方法常用来衡量模型的不确定性, 但是对 LLMs 是否依然适合呢? 作者做了实验, 发现深度集成并没有显著减小认知不确定性, 所以这两种方法失效了. 进一步的, 作者提出了一种对称于 BNN 方法的替代框架

Input Clarification Ensembling

既然集成模型以减小认知不确定性比较困难, 那能修改输入来减小认知不确定性吗?

Excuse? 这样减小的不是偶然不确定性吗

1. Input Clarification: 给定输入 $\boldsymbol{X}$, 生成一系列 “澄清”(clarification) $\boldsymbol{C}^{(k)}$, 这些澄清用于减小输入带来的认知不确定性. 加入澄清后的输入表示为 $\boldsymbol{X}\oplus \boldsymbol{C}^k$, 这里 $\oplus$ 代表 concat 操作. 需要说明的是, $\{\boldsymbol{C}^{(k)}\}$ 是一个集合
2. Ensemble: 输入澄清的分布表示为 $q(\boldsymbol{C}|\boldsymbol{X})$, 模型输出变化为 $q(\boldsymbol{Y}|\boldsymbol{X}) = \mathbb{E}_{q(\boldsymbol{C}|\boldsymbol{X})}[q(\boldsymbol{Y}|\boldsymbol{X}\oplus\boldsymbol{C}, \boldsymbol{\theta})]$

   \mathcal{H}(q(\boldsymbol{Y}|\boldsymbol{X})) = \underbrace{\mathcal{I}(\boldsymbol{Y}; \boldsymbol{C}|\boldsymbol{X})}_{\textcircled1'} + \underbrace{\mathbb{E}_{q(\boldsymbol{\boldsymbol{C}|\boldsymbol{X}})}\mathcal{H}(q(\boldsymbol{Y}|\boldsymbol{X}\oplus \boldsymbol{C}))}_{\textcircled2'}

   上面 \textcircled1' 代表模型输出分布与澄清间的互信息, 可以近似输入模糊性引起的偶然不确定性; \textcircled2' 代表给定不同澄清时的模型输出分布的平均熵, 表示给定澄清后的不确定性, 也即认知不确定性 (这里假设输入模糊性是认知不确定性的唯一来源)

值得注意的是, 以上公式与 Deep Ensemble 的公式具有对称性, 二者分别关注偶然不确定性和认知不确定性, 这分别对应各自公式的第二项

Input Clarification

本文关注由指令模糊性和问题模糊性引起的不确定性, 提出了一个框架

作者表明, 该框架可以很容易地推广到其他输入组件, 如 Instructions, In-Context Examples, Questions. 与这里的整体输入是类似的. (究竟如何, 谁知道呢)

工作的关键在于 clarification 的选择, 文中用一个 clarification LLM 来生成, 所以 $q(\boldsymbol{C}|\boldsymbol{X})$ 其实是 clarification LLM 的输出分布

实际上做的工作类似于, 用户输入指令后, 另一个 LLM 判断下用户的指令是否清晰, 不清晰则生成澄清指令, 从而减小模型的认知不确定性; 或者像作者在 improving performance 里说的, 让用户重新输入

[TMLR202405] Generating with Confidence: Uncertainty Quantification for Black-box Large Language Models

这篇文章指出, 既有研究忽略了不确定性和置信度间的区别, 作者认为置信度是衡量给定响应正确性的更可靠指标

• 置信度: 对特定预测/生成的置信度
• 不确定性: 对固定输入的潜在预测的 “分散程度”

举个栗子, 对于正态分布 $P(Y|x) = \mathcal{N}(\mu, \sigma^2)$, 方差 $\sigma^2$ 可以看成不确定的度量, 对于特定预测 $Y=y$, $-\frac{|y-\mu|}{\sigma}$ 可以看成 confidence 的度量 (或称置信度). 最常用生成序列的联合概率来表示生成的置信度, 表示如下

$C(x, \boldsymbol{s}) = \hat{p}(\boldsymbol{s}|x) = \prod_i \hat{p}(s_i|s_{<i}, x)$

Existing literature sometimes uses uncertainty estimate U (x) to predict the correctness of a particular response s (Kuhn et al., 2023; Malinin & Gales, 2021), ignoring the distinction between uncertainty and confidence. Section 5 shows that this is problematic, and confidence is a more reliable indicator of the correctness of a given response.

论文将模型采样多条答案作为前提, 作者将当前衡量答案相似度的方法分为两类

1. Jaccard Similarity. 具体计算方法是, 两个集合交集的元素数量除以并集的元素数量; 句子/文档视为单词的集合; 这种方法计算效率较高, 但会忽略词序, 无法捕捉否定词的关键信息
   $a_{Jaccard}(\boldsymbol{s}_{j_1}, \boldsymbol{s}_{j_2}) = |\boldsymbol{s}_{j_1}\cap \boldsymbol{s}_{j_2}|/|\boldsymbol{s}_{j_1}\cap \boldsymbol{s}_{j_2}|\in[0, 1]$
2. Natural Language Inference(NLI). 现有的工作大多基于语义熵的 DeBERTa-large 模型来做, NLI 模型预测出 entailment(蕴含), neutral(中立), contradiction(矛盾) 三种答案间的关系

以以上两种相似度度量方法为基础, 作者进一步提出置信度的计算方法, 这里第二种方法也就是作者提出的方法

1. Number of Semantic Sets. 也就是语义熵使用的方法, 计算方法表示为 $U_{\mathtt{NumSet}}$

2. Sum of Eigenvalues of the Graph Laplacian. 实际上, 类别的区分不一定是非黑即白的, 而且 NLI 模型判断的方法不一定有语义等价上的传递性, 我们需要一种更细致且"连续"的方法.

   只知道 Similarity 但不知道 Embedding, 所以可以选择谱聚类 (spectual clustering) 的方法. 将每个答案视作一个节点, 定义加权邻接矩阵 $W = (w_{j_1, j_2})_{j_1, j_2}=1, \dots, m$, 这里 $w_{j_1, j_2} = (a_{j_1, j_2}+a_{j_2, j_1})/2$, 对称归一化图拉普拉斯算子为

   $L := I-D^{-1/2}WD^{-1/2}\\ D_{j_1, j_2} = \begin{cases} \sum_{j'\in[m]}w_{j_1, j'} & (j_1=j_2)\\ 0 & (j_1\neq j_2) \end{cases}$

   语义熵里的与依据类方法是离散的(非黑即白), 其连续化的版本可以用 $L$ 的特征值 $\lambda_1<\cdots<\lambda_m$ 表示

   $U_{\mathtt{EigV}} = \sum_{k=1}^{m}\max(0, 1-\lambda_k)$

   证明略

[ICLR2024 poster] Can LLMs Express Their Uncertainty? An Empirical Evaluation of Confidence Elicitation in LLMs

论文做了一些 rethinking 的工作, 用实验验证了既有的 prompt 策略在 uncertainty 中的作用. 对大模型不确定性的研究给了很多实验补充. 从 prompting, sampling 和 aggregation 三个不确定评估组成部分进行分析. 论文里的方法对所有方法都适用, 但是对 white box 模型研究有所不足.

Contribution 如下:

1. 证明 LLM 往往会过度自信
2. 证明 LLM 模型校准与错误检测水平有限
3. 受人类启发的 prompt, 回答一致性和更好的聚合策略能帮忙缓解这种过度自信
4. 论文提出的方法比不上白盒方法, 但差距较小 (AUROC 从 0.522 到 0.605 很小吗?). 这里的方法是将每个组件与其他部分的组件排列组合得到的

置信度激发 (Confidence Elicitation) 指不进行模型微调或访问内部信息 (包含 token, logit 等等) 情况下估计 LLM 对回答的置信度的过程. 2205的文章《Teaching models to express their uncertainty in words》提出的这个概念. 作者给相关工作了给很多细致的分析, 在附录 C 里.

既有的提示词 (Prompting) 策略可以分为

1. Vanilla, 自己给答案和置信度, 朴实无华. “Read the question, provide your answer, and your confidence in this answer.”
2. CoT, step by step 给出理由. “Read the question, analyze step by step, provide your answer and your confidence in this answer.”
3. Self-Probing, 喂自己的QA对, 再给置信度, 这样能减小一次生成中的过度自信问题. “Question: […] Possible Answer: […] Q: How likely is the above answer to be correct? Analyze the possible answer, provide your reasoning concisely, and give your confidence in this answer.”
4. Multi-Step, 分解推理过程, 得到每部分信息的平均值. “Read the question, break down the problem into K steps, think step by step, give your confidence in each step, and then derive your final answer and your confidence in this answer.”
5. Top-K, 生成最自信的 K 个答案. “Provide your K best guesses and the probability that each is correct (0% to 100%) for the following question.”

文章采用的采样 (Samping) 策略有

1. Self-random. 即多次采样的随机性
2. Prompting. 同一问题的多种表述
3. Misleading. prompt 里给模型误导性的prompt, 用以评估误导信息对模型的作用

文章采用的聚合 (Aggregation) 策略有

1. Consistency. 多次采样回答间的一致性
2. Avg-Conf. 在 consistency 上乘了语义置信度
3. Pair-Rank. (卒)

实验部分值得一看, consistency 要比让模型自己给出置信度更可靠, 符合直觉. 综合下来效果最好的方法是 Top-K prompt + Self-Random sampling + Avg-Conf/Pair-Rank. 聚合策略上, Avg-Conf 更适合检测错误, 预测置信度更适合用 Pair-Rank

有一个观点很有趣: 作者认为, 目前白盒方法和黑盒方法差的不多. 白盒方法中 Length-Normalized Sequence Probability(长度归一化概率, len-norm-prob) 和 Key Token Probability(关键 token概率, token-prob) 效果最好, 但所有方法都有提升空间.

附录里的实验结果表明:

1. prompt 要求 LLM 自信或谨慎, 并不会显著影响结果
2. prompt 要求 LLM 回答出自信度, 这种 verbalizing confidence 会比较高, 置信度普遍为 5 的倍数, 集中在 80% 到 100% 间. 即模型过度自信. 因此多次采样回答的一致性比模型自表达的置信度更可靠
3. 误导性 prompt 分为弱声明 (“我认为答案是…”), 强声明 (“我确信答案是…”), 外部声明 (“维基百科说…”). 弱误导性被纠正的可能性更大, 强声明和外部声明的影响会更大

Self Correct

[ICLR2024 poster] Large Language Models Cannot Self-Correct Reasoning Yet

intrinsic self-correction: 不依靠外部反馈, 模型仅依靠其固有能力纠正初始回答

作者提出, 既有 intrinsic self-correction 方法有效果得益于

1. 使用真实标签作为监督信号. Self Correction 的方法使用真实标签作为监督信号, 当模型回答正确时停止修正
2. 和 self-consistency 方法错误地比较. 将模型答案喂给模型自身, 这与模型生成答案的 “自一致性” 有关, 而不是 self correction 的关系
3. 未选择最优 prompt 设计. 没有要求初始回答的 prompt 设计有缺陷, 从而导致 self correction 效果提升

文章认为, 模型在没有外部反馈时, 不能做到 self correction. 附录给的全是例子

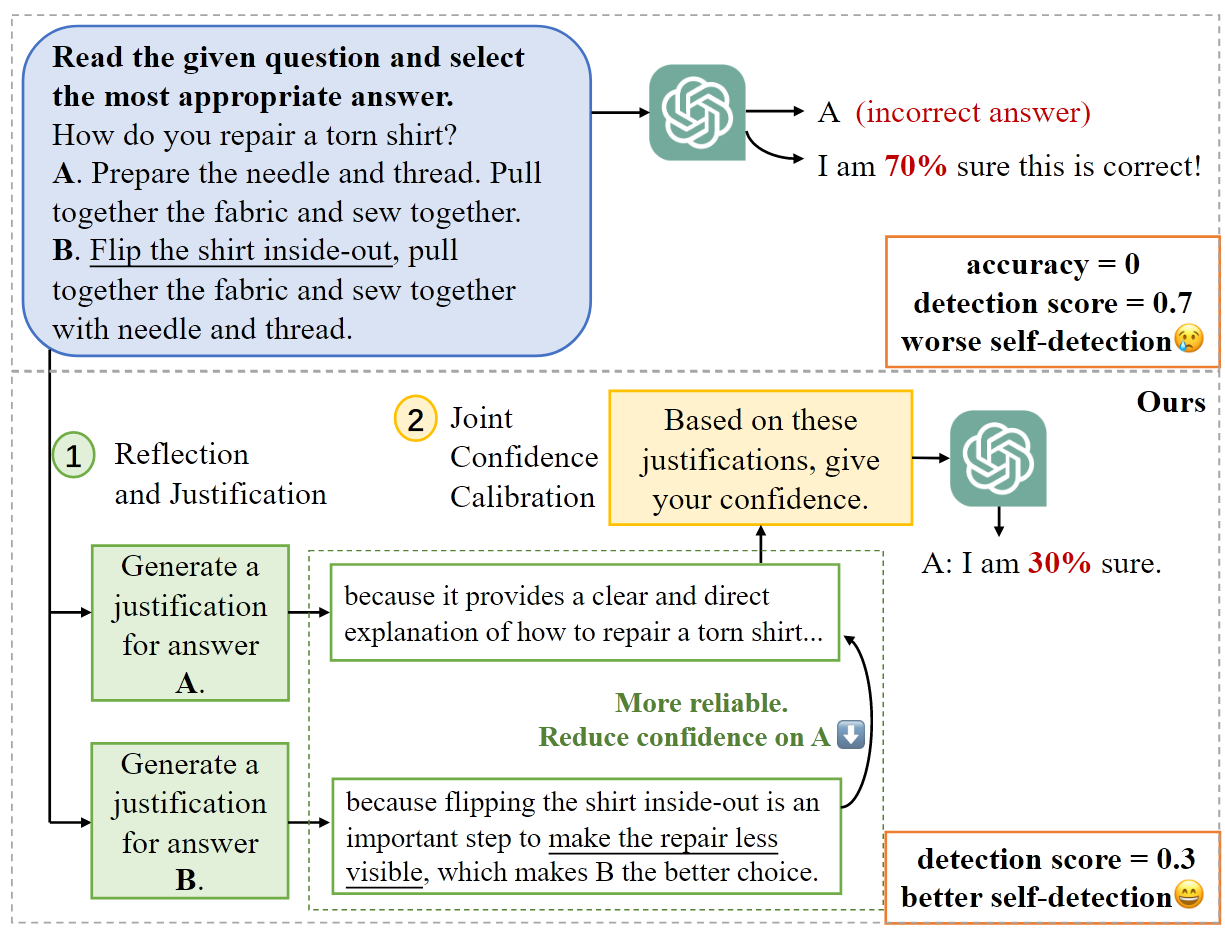
[EMNLP2024 Findings] Think Twice Before Trusting: Self-Detection for Large Language Models through Comprehensive Answer Reflection

Self Evaluation 的范式是将生成的多个答案重新输出模型让模型判断可信度, 是一种类似于 Model Ensemble 的方法. 本文在将模型生成的 Answer 重新输入模型进行判断前, 为每个答案生成 justification, 类似进行了 Joint Confidence Calibration, 再输出 GPT. 这种方法作者自称 Comprehensive Answer Reflection. 论文没有给代码

作者还给了一个 Self Detection 和他们方法范式的对比:

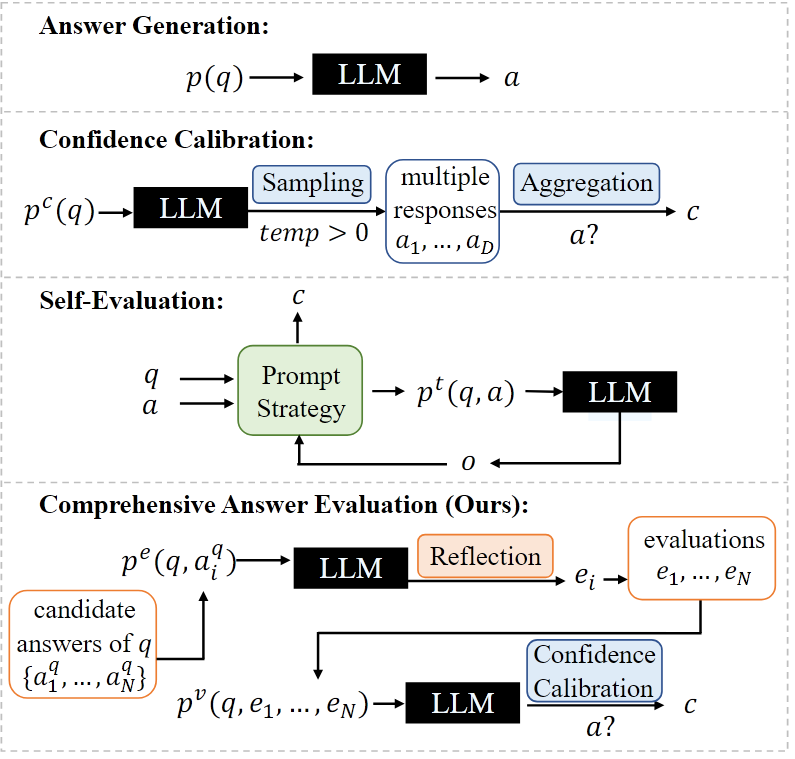
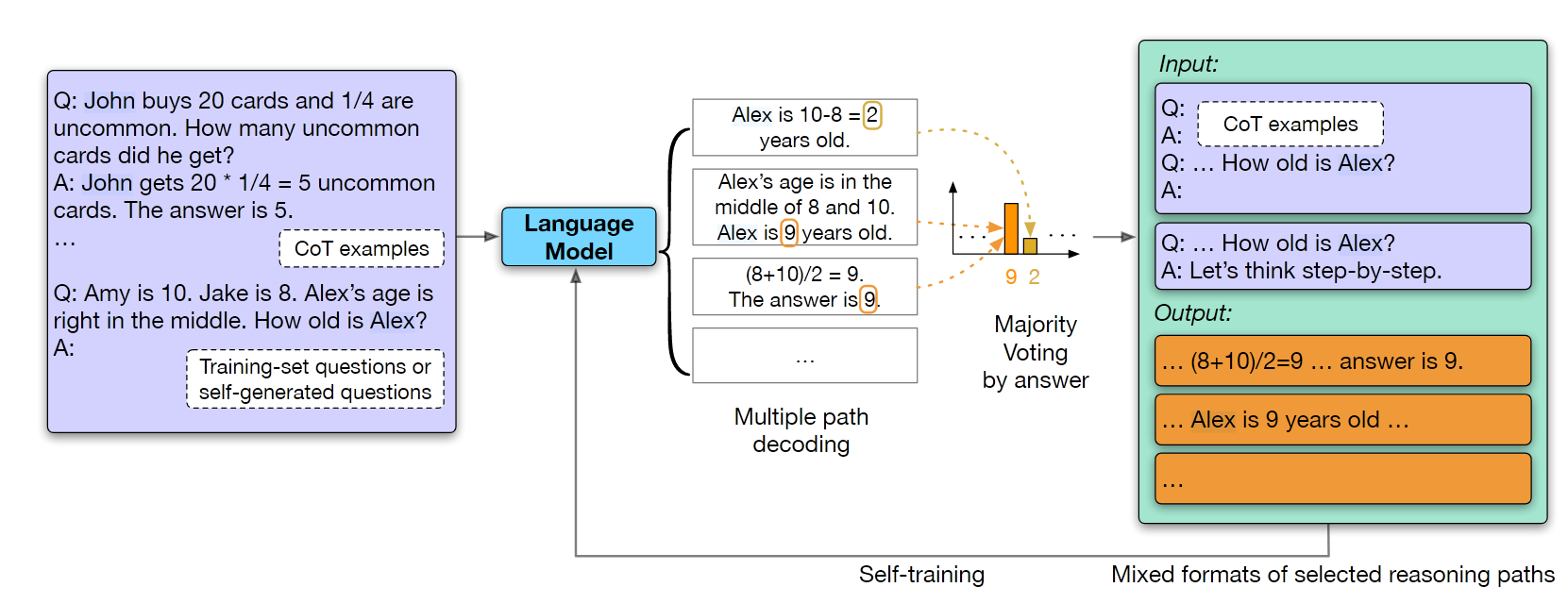
[EMNLP2023 Main] Large Language Models Can Self-Improve

Few-Shot 设置, CoT + Self Consistency 从而得到无标签数据集的标签, 用这个这些数据 finetuning 模型, 可以提高模型性能. 代码未开源

Multimodal

[arXiv:2412.14660v1] Unveiling Uncertainty: A Deep Dive into Calibration and Performance of Multimodal Large Language Models

论文做了一些探索性的工作, 得出了一些显而易见的结论, 有些粗糙, 估计后面还会更新论文

Contribution:

1. MLLMs在微调前后保持相对一致的校准能力. MLLMs训练后对语言任务的校准影响最小
2. MLLMs在文本信息中的不确定性较低. 两种模态信息可以整合以降低模型不确定性
3. 构造了IDK(I dont know)数据集, 这是一个理论上不知道回答的数据集 (OOD数据集). (这种类型数据集在Can ai assistants know what they don’t know? arXiv preprint arXiv:2401.13275.第一次提出)
4. 验证了 temperature scaling 和 iterative prompt optimization 等方法的有效性

MLLMs本身对图像的不确定性就更高; 经过MLLMs第三阶段对LLM的微调后, 模型对图像信息会更自信. 这里实验是将图像换成了文本信息

论文做了一个实验: 给生物图像加了不同级别的高斯噪声, 向这些图像逐步加入多个独立的句子, 每个句子描述该生物的不同特征. 观察这一过程的不确定性变化曲线. 结果蛮符合直觉的: 模糊越多的, 图像不确定性却大; 固定图像, 文本描述越多, 不确定性越大

通过在IDK数据集上的实验表明, 添加如 “If you don’t know the answer, please say…” 的 prompt 是有效的

Temperation Scaling With MLLMs’ Predictive Distribution

指出了一个显而易见的结论, 没什么卵用

Prompt Tuning

这里是用 prompt 显式地对模型进行校准, 比如要求的回答的格式从 “Answer” 换成 “This answer might be…” 或 “This answer must be…” 来减少自信或增强自信

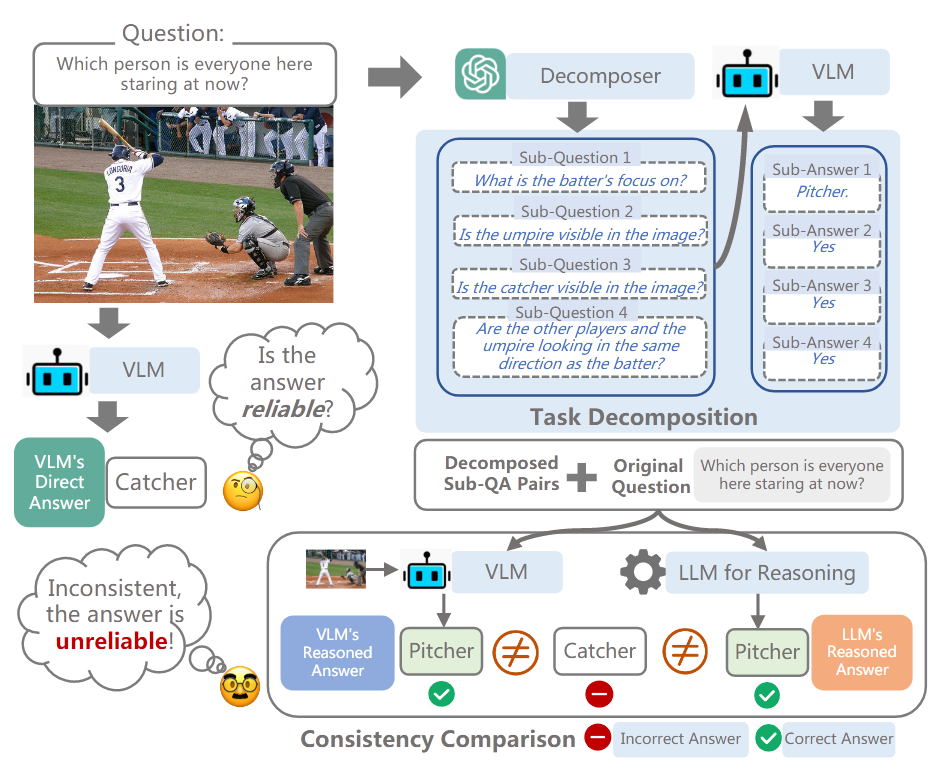
[EMNLP2024 Main] Decompose and Compare Consistency: Measuring VLMs’ Answer Reliability via Task-Decomposition Consistency Comparison

prompt engineering

ICLR2024的 “Large Language Models Cannot Self-Correct Reasoning Yet” 说明了单一模型难以解决认知偏差问题, 因此作者提出多个模型作 multi agent 的方法, 利用额外的 LLM 和 VLM 来验证单一 VLM 的结果. 通过将 question 分解成 sub-question, 利用额外的 VLM 回答 sub-question, 并用额外的 LLM 整合所有的 sub Q-A pairs, 来验证 VLM 回答的正确性

验证指标

论文的验证指标是 Briear Score(BS) 和 Effective Reliability(ER). 下面 $\mathcal{R}_i$ 是表示验证结果是否一致的二元变量, $N$ 是数据集大小, $Acc$ 表示真实预测准确率. 指标越小表示验证结果越准确. 附录里还有提没有使用 ECE(Expected Calibration Error) 和 C@R 的原因

$\mathrm{BS} = \frac{1}{N}\sum_{i=1}^{N}(\mathcal{R}_i-Acc_i)^2\\ \mathrm{ER}(A_i) = \begin{cases} 1 & \text{if } R_{ij} = 1 \text{ and } Acc_{i} = 1 \\ -1 & \text{if } R_{ij} = 1 \text{ and } Acc_{i} = 0 \\ 0 & \text{if } R_{ij} = 0 \text{ (answer abstention)} \end{cases}$

比较方法

1. 直接回答的困惑度 Perplexity of Direct Answer: 计算直接回答的 token 的平均困惑度, 并设置阈值判定一致性
2. 大模型生成的置信度 Generated Numerical Confidence: 利用 prompt 让 VLM 生成一个置信度和回答, 回答格式是 “Answer: X. Confidence: X%”, 这里回答的 Confidence 是连续的 (尽管生成并不是连续的)
3. 大模型生成的语义置信度 Generated Linguistic Confidence: 利用 prompt 让 VLM 表示回答是否自信, 回答是二元而非连续的
4. 回答一致性 Self-Consistency based on Paraphrase: 大模型将问题转换为语义相同的其他表达, 并用 VLM 回答, 如果有与原答案不同的回答则判定不一致

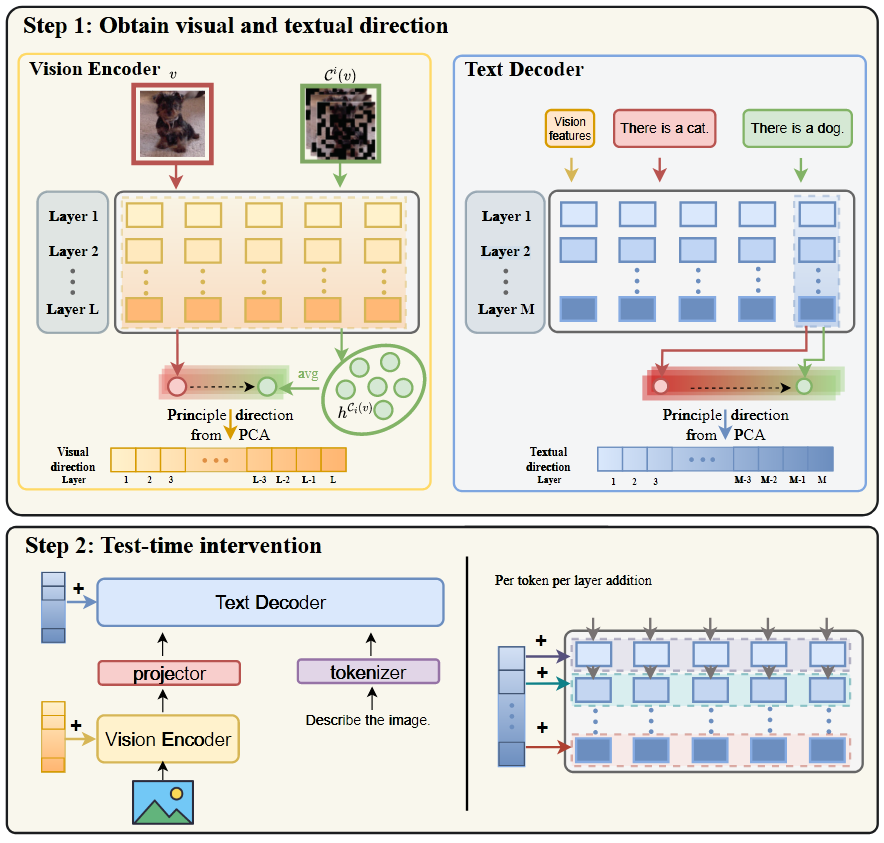
[ICLR2025 spotlight] Reducing Hallucinations in Large Vision-Language Models via Latent Space Steering

代码未开源, openreview 上还没传最终版本. 论文方法写的不清楚

Contribution:

1. 证明视觉特征稳定有利于减小 LVLMs 幻觉
2. 提出 VTI(Visual and Textual Intervention), 在隐空间中生成输出

证明视觉特征稳定有利于减小幻觉

针对 object hallucination 研究特征稳定性与物体幻觉关系的实验里, 作者给原始图像添加了多种类型的噪声, 分析了由此产生的特征分布方差. 大意是, 加噪过程中改变了图像的某些视觉特征, 从而使视觉特征分布的方差明显变大, 这说明部分视觉特征对幻觉产生的影响更大; 给相同的图片加上采样自同一分布的不同噪声, 然后将这些加噪后的图片做 pixel-wise 的平均, 对平均后的图片再做 QA, 幻觉比加噪平均前的图片要少 (?). 我的理解是: 每次加噪都会影响一部分视觉特征, 但是同一分布采样的所有噪声累加的结果相当于一次噪声, 且等价噪声扰动的是更重要/high level的视觉特征 (像是正态分布的采样累加更接近标准正态分布一样), 所以 pixel-wise 均值的 embedding 出现幻觉的可能性比单个加噪要小

没太读懂这里的方差和视觉特征的平均化处理是什么意思, 原文翻译如下:

为了研究特征稳定性与物体幻觉之间的联系，我们对原始图像施加了多种类型的噪声，并分析了由此产生的特征分布的方差。理想情况下，如果视觉编码器足够鲁棒且经过有效训练以捕捉语义信息，那么不会改变图像语义内容的噪声对视觉特征或模型输出的影响应该是最小的。

然而，如图2左图所示，尽管大多数视觉特征保持稳定，但约有15%的特征表现出显著的方差，形成了长尾分布。这些不稳定的特征与幻觉密切相关，因为模型对这些特征过于敏感，导致其输出不准确。这种关联在图2的第二幅图中得到了进一步证明：通过对多个注入噪声的图像进行视觉特征的平均化处理，随着扰动次数的增加，幻觉现象减少，无论注入的噪声类型如何。重要的是，如右图所示，这种减少并非由噪声本身引起，而是由于对扰动的平均化处理，而单独使用噪声往往会增加幻觉现象。

VTI (Visual and Textual Intervention)

先计算稳定图像特征的向量, 然后将其应用于测试过程, 同理文本方向. 相当于在编码器每一层给 token 加一个偏移向量, 偏移向量是作者在自己设计的数据集上计算出来的固定值, 计算后可用于所有样本推理

偏移向量的计算方法与使用:

1. 给图片随机 mask, 得到其 embedding $h_{l,t}$, 根据上面的探索性实验, 可以认为该图片的鲁棒性 embedding 是所有掩码图像 embedding 的平均值 $\overline{h}_{l, t}$. 用 $\Delta_{l, t}^{v_i}$ 作为该图片的偏移向量, 每个元素是一次随机掩码处理后的结果
2. 为了避免 data-specific, 自制数据集重复以上过程, 偏移向量即$d_{l,t}^{\mathrm{vision}} = [\Delta_{l, t}^{v_1}, \Delta_{l, t}^{v_2}, \cdots, \Delta_{l, t}^{v_N}]$, 这里 $N$ 是自制数据集样本数