forum?id=ki4R0z0C4K&referrer=Author Console)

Swin Transformer

ViT 与 Swin Transformer

首先介绍 VIT 和 Swin Transformer 的区别

ViT 执行全局注意力机制, 计算了所有 tokens 之间的关系. 这种全局计算导致了与 token 个数二次相关的复杂度
Swin Transformer 执行局部窗口自注意力机制, 计算了窗口内所有 tokens 间的关系, 降低了计算复杂度

假设一个图像分为 $h*w$ 个 patch, 窗口大小为 $M$ . 二者的计算复杂度为:

\Omega(W-MSA) = 4hwC^2 + 2M^2hwC

Linear 的参数量为 $in\_features\_num \times out\_features\_num$ , 计算量为 $bs\times features\_dimensions\times in\_features\_num \times out\_features\_num$

(a, b) 与 (b, c) 的矩阵相乘, 计算量为 $abc$

MSA 内, 生成 QKV 时 $Q = x\times W^Q$ , $x$ 的维度是 $(hw, C)$ , $W$ 的维度是 $(C, C)$ , 所以这三项的复杂度是 $3hwC^2$ ; 计算注意力矩阵时的复杂度是 $(hw)^2C$ ; 忽略 softmax 的计算复杂度, softmax 后乘 $V$ , 计算复杂度是 $(hw)^2C$ ; 经过变换得到最终输出, 复杂度是 $hwC^2$ .

W-MSA 内, 生成 QKV 和矩阵变换得到最终输出的计算复杂度与 MSA 一样为 $4hwC^2$ ; 计算窗口自注意力时共有 $\frac{h}{M}\times\frac{w}{M}$ 个窗口, 每个窗口的计算复杂度为 $(M^2)^2C$ , 注意力矩阵与 $V$ 相乘, 这部分计算复杂度为 $M^2hwC$ .

值得注意的是, Swin Transformer 的计算复杂度是随着图片大小增加而线性增长的. Swin Transformer 有了类似卷积神经网络那样多尺度的特征, 所以很容易用到下游任务上

Swin Transformer 的循环移位窗口与掩码方法详解

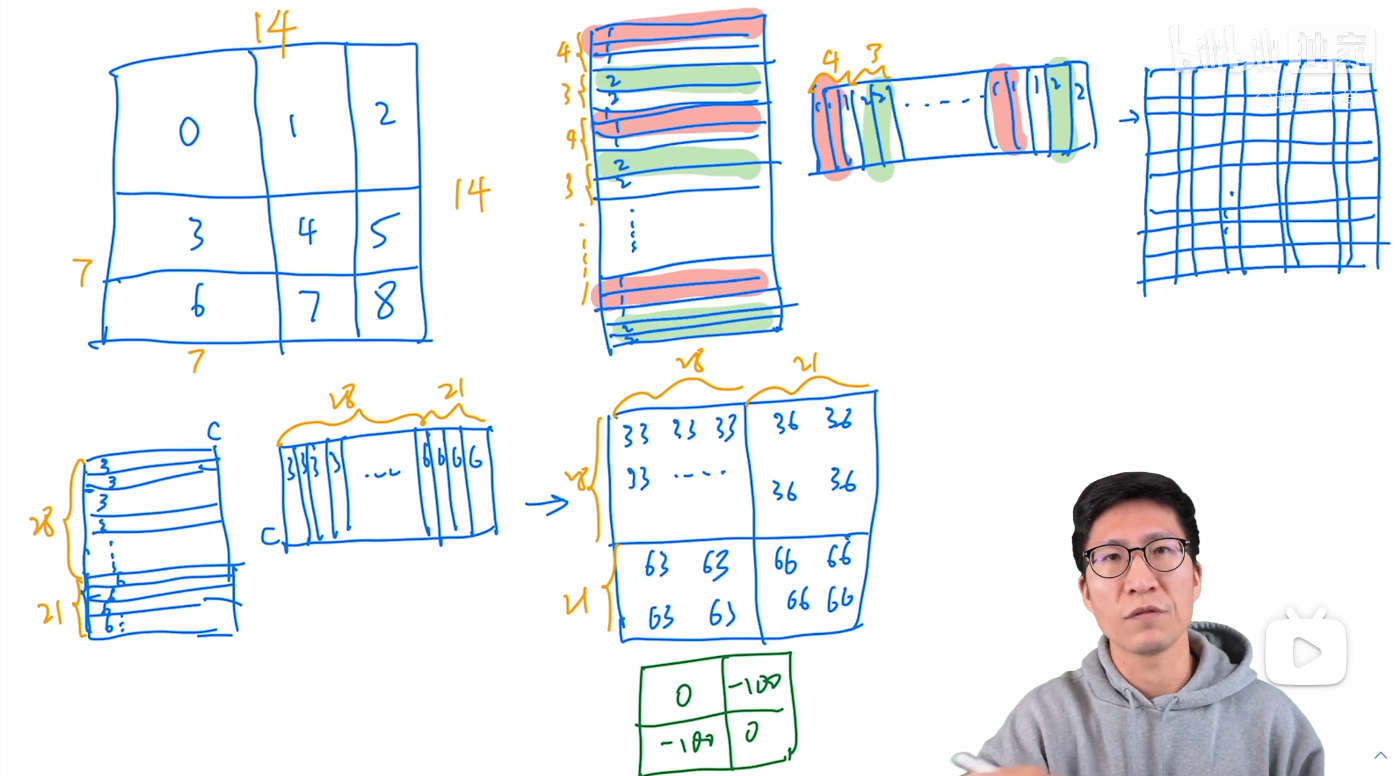
在循环移位中的掩码操作如下, 右图是每个窗口内计算出的 attention map

Swin Transformer 的掩码操作

我之前疑惑的地方在于, 这个掩码是操作的? 为什么移位后就能加掩码了? 在 NLP 里了解了 Attention Mask 后有了更深刻的理解. 我们所说的掩码其实都是在 Attention Matrix 上操作的, 将一个大小相同的掩码矩阵与 Attention Matrix 相加, 掩码矩阵中想要被关注/保留的内容为 0, 不想关注/保留的内容值为一个很小的数, 如 -100. 这样实现了对于无关内容的忽略.

关注完窗口循环移位与掩码操作后, 思考下为什么这里要进行这样的操作? 我们注意到 Swin Transformer 论文的第二张图片, 也就是下面这张图. 可以看到, 没有滑动窗口机制时窗口数量为 4, 如果移位后补 padding, 窗口数量是9, 计算量提升了 2.25 倍. 所以循环移位和掩码的操作目的是为了减少计算量, 用 4 个窗口的计算实现 9 个窗口计算的作用.

为什么不使用全局注意力

Swin 本身就是一个层级的结构, 提取到了多尺度特征, 某一层中应当考虑同一尺度的特征.

考虑到窗口自注意力是在窗口内计算的, 这里是窗口的尺度. 如果使用 self attention 的全局注意力, 那依然存在计算量成平方的问题, 而且这里不能以窗口为单位进行全局注意力的计算注意力, 只是像素层面上的计算, 所以也没有选择.

全局卷积核没有在空间上计算?

是的, 在通道上进行的注意力计算, 算是变相的加参数.

Uformer 的创新点是什么?

在 Decoder 的 Attention 模块上加入了 modulator. 图像退化的方式不同, 为了提高处理各种退化的能力.

modulator 是 $M\times M\times C$ 形状的可学习张量, $M$ 为窗口大小, 每个 modulator 作为一个共享偏置项 (每一层中加到每个窗口上的 modulator 相同, 不同层的 modulator 不同)

多尺度噪声项加入到 feature map 中, 实现随机变化已生成更逼真的图像

有没有试过只用我们自己的模块?

我们的模块是在 SW-MSA 上进行的补足, 所以要和 SW-MSA 一起使用效果会更好. 单独使用效果不会更好

针对多模态大模型的图像信息补足

attention value 小可以说明图像信息的丢失吗?

不能直接说明, 但是可以由此推出图像信息丢失, 作者进一步作实验证明了图像信息在前几层向 text tokens 的转移. 但是这种转移过程存在信息的不完全转化的问题 (就像模型训练那样, 这在大模型中更甚), 图像信息可能在转移过程中丢失或被遗忘.

或者讲, 当前并不能做到完全的信息转移与模态对齐. 其中存在图像信息丢失或遗忘的可能. 我们补足的实验证明了这种可能性.

为什么不在每一层 TransformerBlock 里或者每一层 TransformerBlock 后面加一个类似的模块

没卡
操作复杂, 不能最大化的利用既有的 LLM

为什么一定是在 LLM Backbone 后面加 PIB?

这里我们受到了 HallE-Switch 这篇文章的影响

如果更换 softmax 是否就不会出现 vision tokens 受到的注意力小的现象?

训练问题

损失函数

使用的 HA-DPO 数据集, 所以使用 DPO 的训练方法

DPO 将SFT 后的模型本身作为奖励模型, 但是参数不更新, policy 模型也是本身, 但是参数更新. DPO 的目的是最大化奖励模型, 使得奖励模型对 chosen 和 rejected 的差值最大, 这样模型可以学到人类偏好.

DPO 的 loss 公式:

\mathcal{L}(\pi_{\theta};\pi_{\mathrm{ref}}) = -\mathbb{E}_{(x, y_w, y_l)\sim\mathcal{D}}[\mathrm{log}\sigma(\beta\mathrm{log\frac{\pi_\theta(y_w|x)}{\pi_{\mathrm{ref}}(y_w|x)}-\beta\mathrm{log}\frac{\pi_{\theta}(y_l|x)}{\pi_{\mathrm{ref}}(y_l|x)}})]

以上公式等价于最大化以下部分:

\beta\mathrm{log\frac{\pi_\theta(y_w|x)}{\pi_{\mathrm{ref}}(y_w|x)}-\beta\mathrm{log}\frac{\pi_{\theta}(y_l|x)}{\pi_{\mathrm{ref}}(y_l|x)}}

熵, 交叉熵, KL 散度,

熵

熵的意义是事件 $A$ 的信息量, 越不可能的事件信息量越大, 独立事件的信息量可以叠加

s(X) = -\sum_i P(x)\mathrm{log}P(x)

交叉熵

note: 交叉熵有负号, 其他的没有

离散形式, 对于两个离散概率分布 $P$ 和 $Q$ , $P(i), Q(i)$ 是真实分布 $P, Q$ 在事件 $i$ 上的概率,

H(P, Q) = -\sum_{i}P(i)\mathrm{log}Q(i)

连续形式, $p(x), q(x)$ 分别是真实分布 $P$ 和模型预测分布 $Q$ 的概率密度函数:

H(P, Q) = -\sum_i p(x)\mathrm{log}q(x)dx

性质:

非负性
非对称性
与 KL 散度的关系: 交叉熵可以看做 KL 散度加上真实分布 $P$ 的分布, 即:

KL 散度

KL 散度 (Kullback-Leibler Divergence) 用于度量两个分布间的相似性

离散形式, 其中 $P(i)$ 和 $Q(i)$ 分别是分布 $P$ 和 $Q$ 在事件 $i$ 上的概率

D_{KL}(P\|Q) = \sum_{i}P(i)\mathrm{log}\frac{P(i)}{Q(i)}

连续形式, 其中 $p(x)$ 和 $q(x)$ 分别是分布 $P$ 和 $Q$ 的概率密度函数:

D_{KL}(P\|Q) = \int_{-\infty}^{+\infty}p(x)\mathrm{log}\frac{p(x)}{q(x)}dx

KL 散度的性质:

非负性, KL 散度总是非负的
不对称性, $D_{KL}(P\|Q)\neq D_{KL}(Q\|P)$
非度量性, 不是严格意义的距离度量函数

KL 散度与交叉熵的关系

D_{KL}(P\|Q) = H(P, Q) - S(P)

其中 $S(P)$ 是分布 $P$ 的熵, $H(P, Q)$ 是两个分布的交叉熵.

需要注意, 熵是一个常量, 也就是说 KL 散度和交叉熵在特定条件下等价. 为什么可以使用交叉熵作为损失函数? 因为训练数据的熵是固定的, 所以最小化交叉熵等价于最小化 KL 散度, 目的是让模型处理后的数据更接近真实数据分布