MoE in LLMs(Mixture of Experts)

Motivation

既有数据集特征与标注的关系大有不同, 既有LLMs训练与推理难度大. 为了实现LLMs的高效训练与推理, 有以下几种方法

  • 改变底层模型架构,Transformer -> 基于状态空间模型(SSM)的mamba架构
  • 预训练微调方法, 如URIAL方法
  • MoE基于门控网络的混合专家模型

MoE经典论文一览

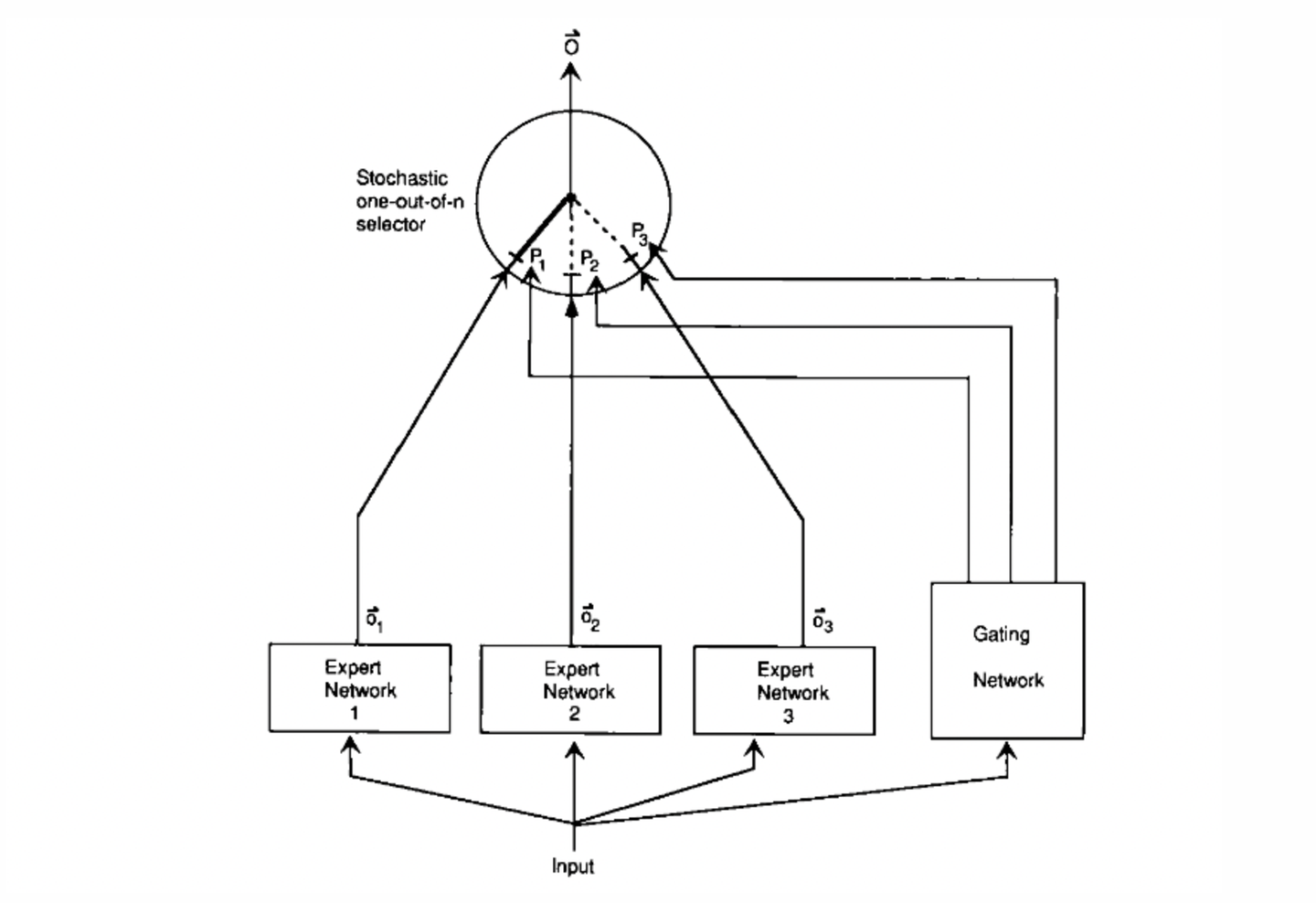
1. Adaptive mixtures of local experts

作者Michael Jordan, Geoffrey Hinton

Motivation

假设数据集中存在不同domain和不同topic的子集, 用单个模型去学习会有很多干扰.

Method

提出一种新的监督学习过程, c.

那么多个模型(expert)去学习, 使用一个门网络(gating network)决定每个数据应该被哪个模型训练, 可以减少不同类型样本间的干扰

更改损失函数

Ec=∥d−∑ipicoic∥2E^c = \|\textbf{d} - \sum_ip_i^c \textbf{o}_i^c\|^2

为

Ec=∑ipic∥dc−oic∥2E^c = \sum_ip_i^c\|\textbf{d}^c - \textbf{o}_i^c\|^2

expert间从鼓励合作变成鼓励竞争, 而且单个expert的值改变不用影响其他expert. pp是门控网络分配的权重, 和experts一起训练

img

2. Outrageously Large Neural Networks: The Sparsely-Gated Mixture-of-Experts Layer

谷歌英国团队2017年的工作, 也有Quoc Le和Hinton的参与

Motivation

想要在有限的计算成本内提高model scale

Method

提出Sparsely-Gated Mixture-of-Experts layer

两个不同:

  1. Sparsely-Gated: 不是所有expert都会起作用, 只有极少数的expert会被用来推理
  2. token-level: 97年的文章是sample-level, 本篇token-level, 一个句子中不同的token使用不同的experts

具体的操作是在RNN结构上加入MoE Layer

img

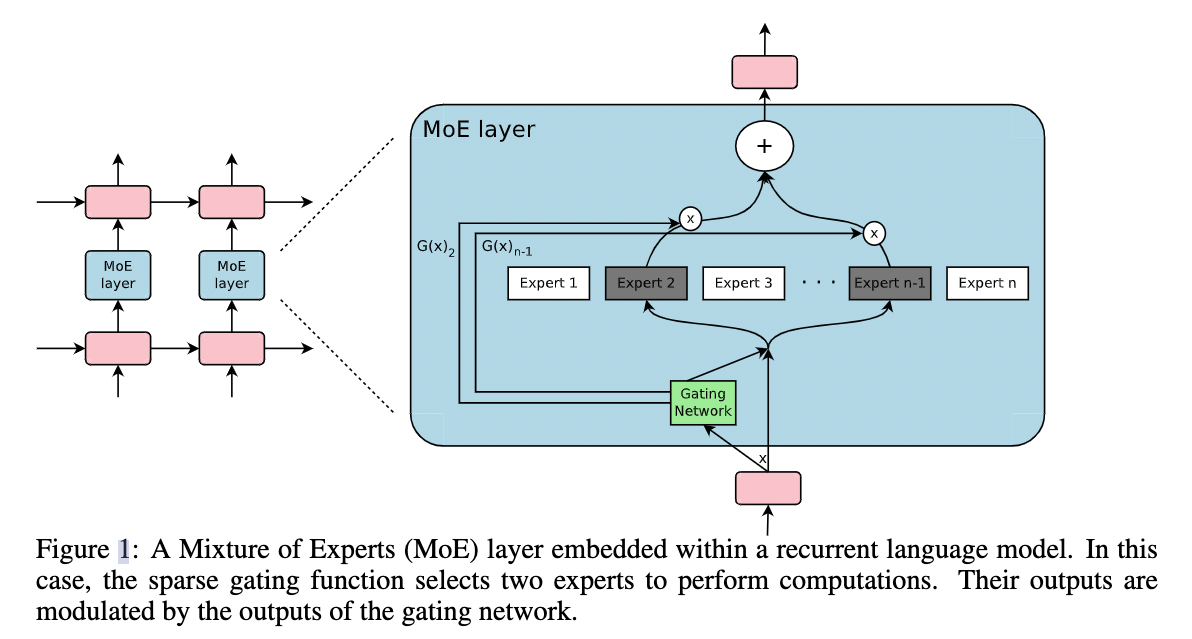
Gating Network

传统门控网络的输出是所有experts的加权和

y=∑i=1nG(x)iEi(x)y = \sum_{i=1}^n G(x)_iE_i(x)

作者加入了sparsity和noise

G(x)=Softmax(KeepTopK(H(x),k))G(x) = Softmax(KeepTopK(H(x), k))

H(x)i=(x⋅Wg)i+StandardNormal()⋅Softplus((x⋅Wnoise)i)H(x)_i = (x \cdot W_g)_i + StandardNormal() \cdot Softplus((x \cdot W_{noise})_i)

KeepTopK(v,k)i={viif viintopKelements−∞otherwiseKeepTopK(v, k)_i = \begin{cases} v_i & \text{if } v_i in topK elements \\ -\infty & otherwise \\ \end{cases}

实验中作者使用的KK在2-4间

Expert Banlancing

存在可能只有少数几个expert起作用的结果, 额外增加一个loss来缓解这个问题

Importance(X)=∑x∈XG(x)Importance(X) = \sum_{x\in X}G(x)

L(X)=λ⋅CV(Importance(X))2L(X) = \lambda\cdot CV(Importance(X))^2

XX表示一个Batch的样本, 把一个Batch的gating weights加起来, 计算变异系数(Coefficient of Variation, 反映离散程度, 原始数据标准差与原始数据平均数的比, 去除量纲影响), 反应不同experts间不平衡的程度, loss加到总体loss中, 鼓励不同的experts发挥各自的作用

3. GShard: Scaling Giant Models with Conditional Computation and Automatic Sharding

谷歌2021年的工作

GShard, 自称第一个将MoE思想拓展到Transformer上的工作. 做法是在Transformer的encoder和decoder中, 每隔一个FFN换成position-wise的MoE层, k=2

img

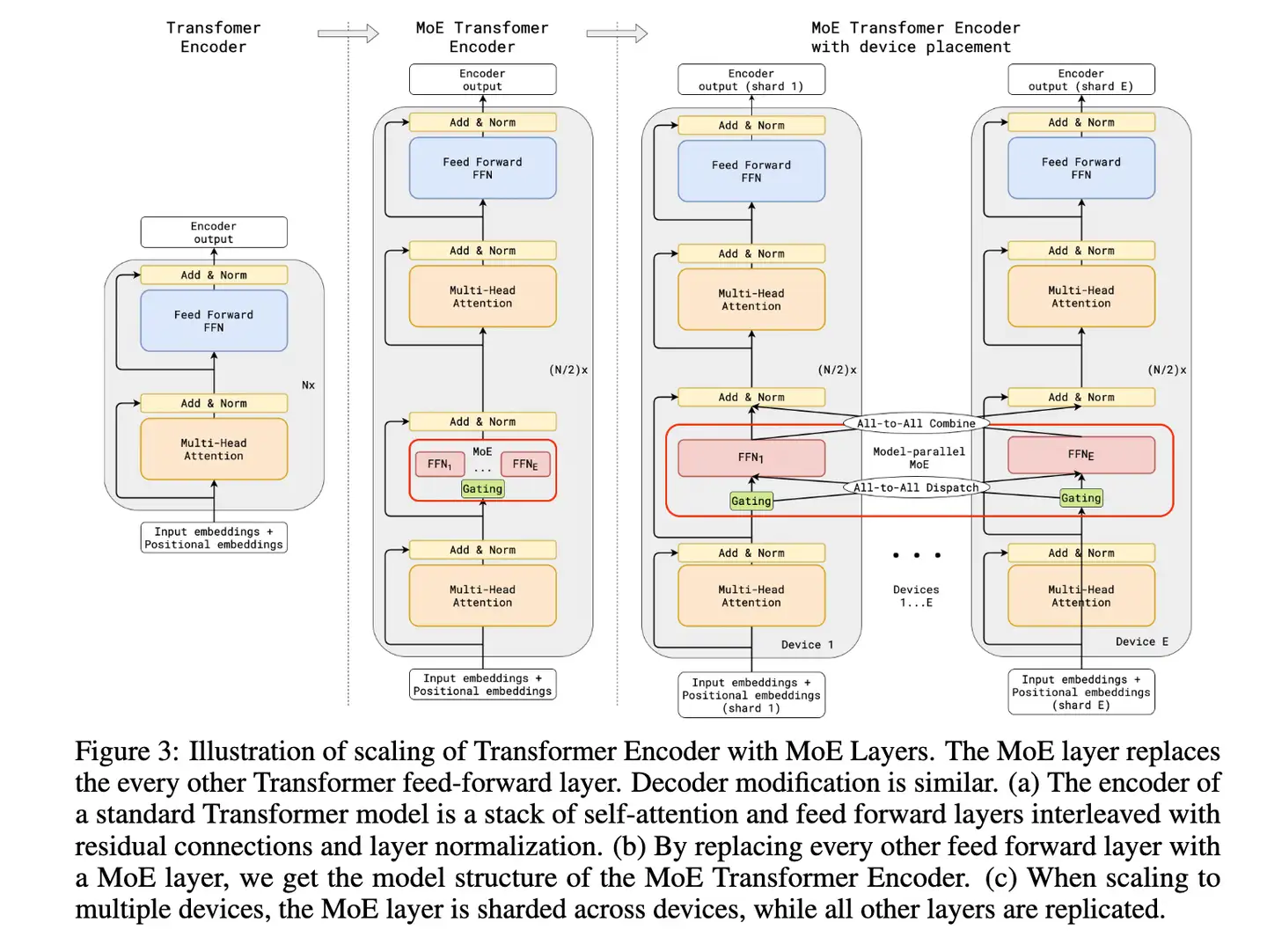
Expert capacity balancing：强制每个expert处理的tokens数量在一定范围内

Local group dispatching：通过把一个batch内所有的tokens分组，来实现并行化计算

Auxiliary loss：也是为了缓解“赢者通吃”问题, 与97年的文章类似

Random routing：在Top-2 gating的设计下，两个expert如何更高效地进行routing

4. Switch Transformers: Scaling to Trillion Parameter Models with Simple and Efficient Sparsity

谷歌团队2021年的工作. 在T5模型基础上加入MoE设计, 在C4数据集上预训练

Motivation

MoE的方法带来了训练和推理的不确定性, 通信成本高等问题

Method

SwitchTransformer使用MoE替代了FFN, 只使用了单专家的策略, 保留了expert balance的辅助损失函数(和其他模型比更稀疏)

减少了Gate的计算, expert训练的bs减半, communication cost(分布式训练中, 不同设备的模型参数要保持一致, 设备间梯度传输)下降

探讨Expert Capacity

Expert_Capacity=(token_per_batchnumber_of_experts)⋅Capacity_factorExpert\_ Capacity = (\frac{token\_ per \_ batch}{number\_ of\_ experts}) \cdot Capacity\_ factor

设置CapacityfactorCapacity_factor在1-1.25间

5. GLaM: Efficient Scaling of Language Models with Mixture-of-Experts

谷歌团队2021年的工作, 使用Sparse MoE使得训练成本只有GPT-3的三分之一, 结构与GShard基本一致

动图

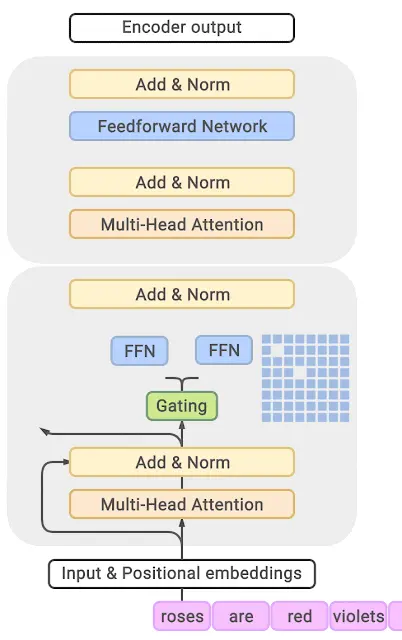
GShard, Switch-Transformer, GLaM都是把模型做大(几百个几千个experts)

6. Go Wider Instead of Deeper

NUS的团队

Motivation

训练和推理过程中, 需要并行地保存参数, performance不能被线性的提升

基于MoE的模型的稀疏性不能在相对较小的数据集上扩展

如何在压缩模型参数量的情况下取得更好的效果?

Method

深度上参数共享, 来压缩模型大小, 宽度上使用MoE的设计(所有FFN替换为MoE), 扩大模型容量

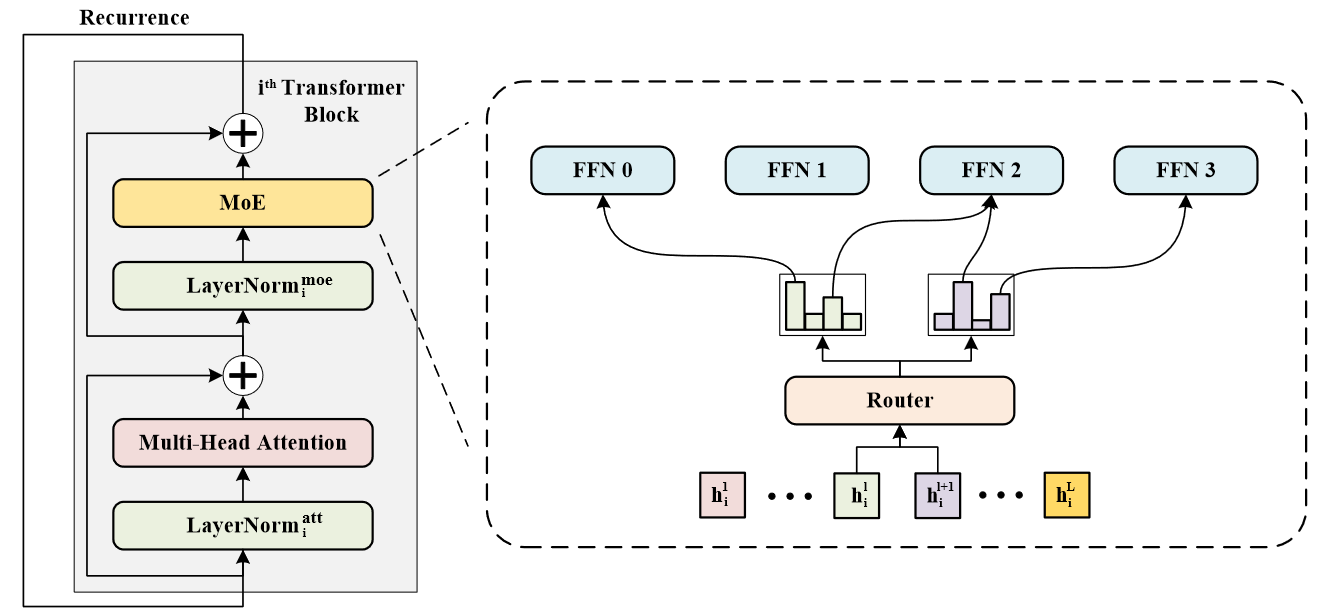
image-20240212135752426

recurrence机制

recurrence机制: 共享参数. 这里只有nomalization layer不共享参数, 用以建模不同的语义信息

使用4个experts, K=2

Balanced Loading

将Balanced Loading归结为解决两个问题

  • 分派单个expert的token过多
  • 分派单个expert的token过少

解决分配过多: 每个expert最多分配B个token, 有

B=CKNLB = CKNL

CC为超参数, 控制每个expert保留token的比例; KK为每个token选择的专家数量; NN为batch size; LL为每张图像中patch token的数量

解决分配过少: softmax(topk())的传统方法

7. MoEBERT: from BERT to Mixture-of-Experts via Importance-Guided Adaptation

Motivation

在MoE大模型结合知识蒸馏时, distillation(蒸馏)方法效果较差

Method

将预训练好的模型的FFN层分解成多个experts, 这样计算时的速度可以大幅提高(相当于只激活原始FFN网络的一部分). 然后再将原始模型的知识蒸馏到MoE版本的模型中

与WideNet的区别: 二者都是为了减少参数量. WideNet是自己从头训练的, MoEBERT想把pre-train好的模型迁移过来, 通过蒸馏的方式在下游任务上学习

expert routing没有用门控网络, 而是训练前使用哈希函数给每个token随机分配了一个expert

Importance-Guided Adaptation

将FFN改造成MoE Layer时, 计算FFN Layer各个neuron的importance. 重要的neurons在每个expert中共享, 剩下的部分平均分配到每个expert

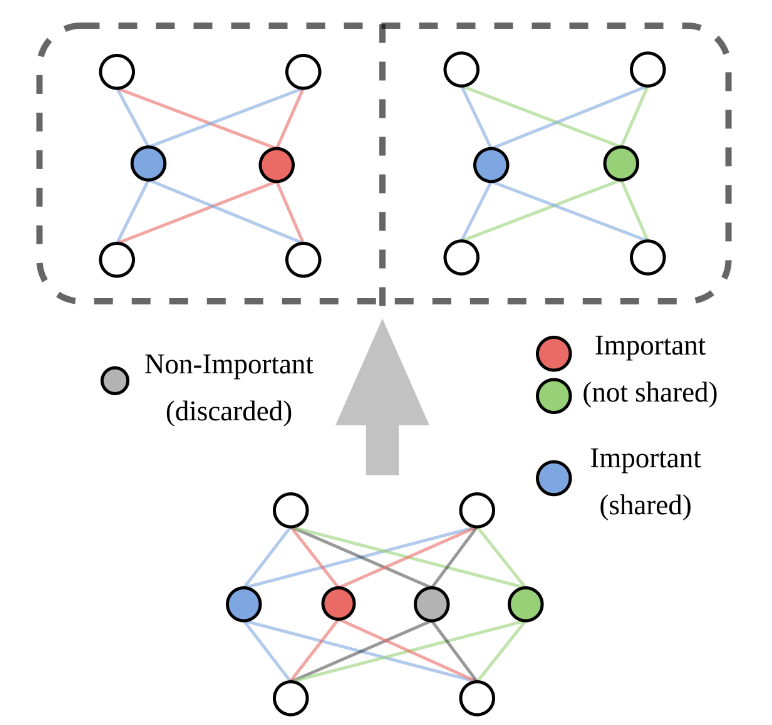
image-20240213105522896

8. Scaling Vision with Sparse Mixture of Experts

谷歌英国团队2021NIPS上的工作

Method

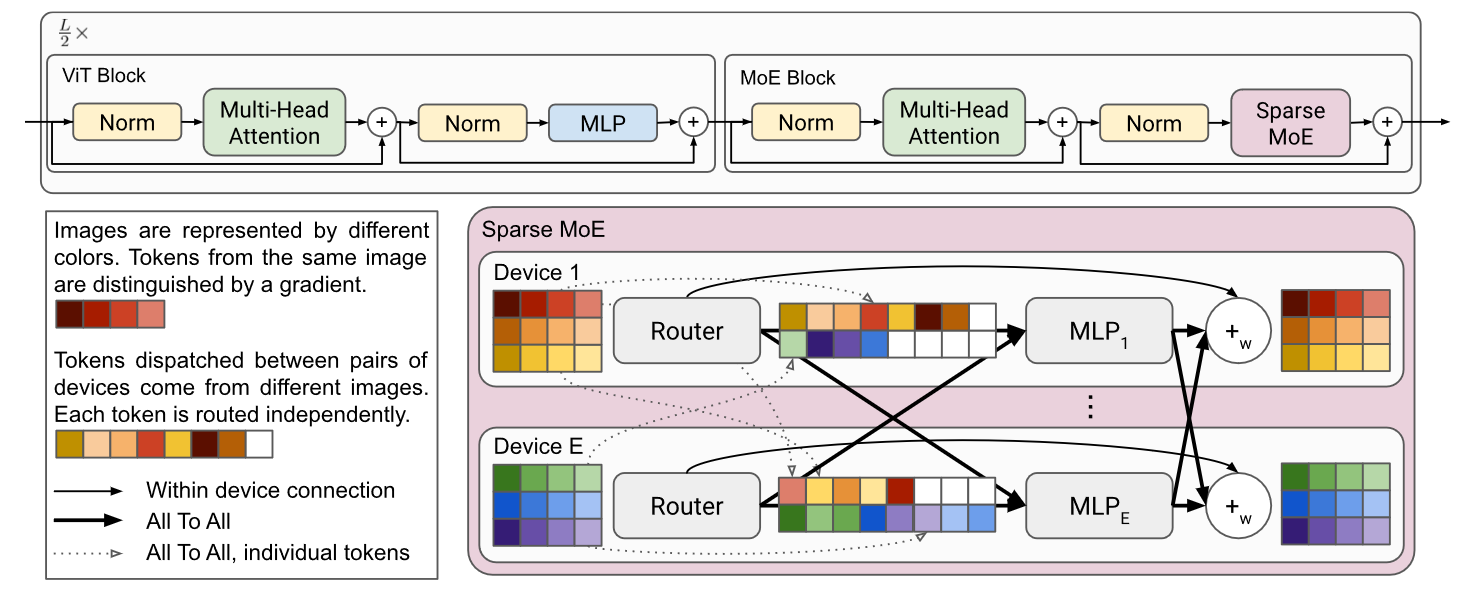
image-20240215140319345

利用模型的稀疏性跳过某些patch的计算, 减少对不提供信息的图像区域的计算

routing

g(x)=TOPk(softmax(Wx+ϵ ))g(\textbf{x}) = \textbf{TOP}_{\textbf{k}}(\textbf{softmax(\textbf{Wx}+$\epsilon$ )})

这里routing选择先softmax再topk使得k=1时也可以训练, 否则梯度会处处为0

Expert’ s Buffer Capacity

Be=round(kNPCE)\textbf{B}_{\textbf{e}} = \text{round}(\frac{\text{kNPC}}{\text{E}})

N\text{N}是batch数, P\text{P}是每个图像的token数量, k\text{k}是每个token选定的expert数量, E\text{E}是experts数量, C\text{C}是容量比率

Be\textbf{B}_{\text{e}}是单个expert最多处理的tokens个数, 这里剩余的tokens并不完全丢掉

BPR(Batch Prioritized Routing Algorithm)

对tokens进行重要性排序, 丢弃无用的tokens

g(x)t, i表示第t个token和第i个expert的路由权重\text{g}(\textbf{x})_{\text{t, i}}表示第t个\text{token}和第i个\text{expert}的路由权重

根据token的最大路由权重对token进行排序, s(x)t\text{s(\textbf{x})}_{\text{t}}代表每个token的优先级分数

s(x)t= maxig(x)t, i\text{s(\textbf{x})}_{\text{t}} \text{= \textbf{max}}_{\text{i}}\text{g(\textbf{x})}_{\text{t, i}}

BPR选择合适的tokens, 变相提供了一种减少缓冲大小的方法

9. Multimodal Contrastive Learning with LIMoE：the Language-Image Mixture of Experts

来自谷歌2022NIPS的工作, LIMoE同时处理文本和图像

Motivation

多模态的MoE存在问题: 模态失衡, 训练集中图片与文本的比例会很大程度影响训练结果

Method

没有采用MLLM常用的每个模态一个网络的方法.

将稀疏化方法用在图像文本模型上, 采用对比学习方法让图像-文本表示更接近. 训练中图像比文本要多, 所有expert都会处理一些图像

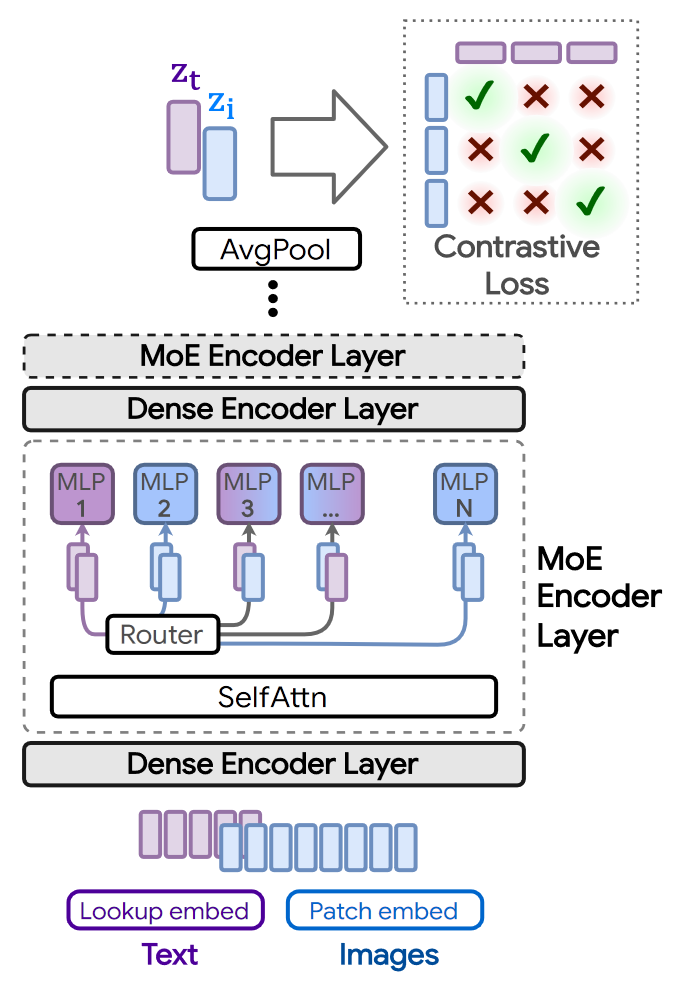
image-20240214201127560

MoE与集成学习的区别

实现方式上, 集成学习不需要将任务分解为子任务, 而是将多个基础学习器组合

img

MoE发展的愿景与困难

愿景

  1. MoE的架构更难训练, 要调的地方很多
  2. MoE的架构有复杂度的下限, 很难蒸馏到非MoE的结构
  3. experts的数量需要适当增加, 否则没办法route到合适的expert

困难

  1. 训练MoE存在很大的困难
  2. 需要合适的Expert Routing Method

MoE在LLMs上的发展

参考链接

大模型LLM之混合专家模型MoE（上-基础篇） - 知乎 (zhihu.com)

Mixture-of-Experts (MoE) 经典论文一览 - 知乎 (zhihu.com)

万字长文详解 MoE - 超越ChatGPT的开源混合专家模型 - 知乎 (zhihu.com)

大模型的研究新方向：混合专家模型（MoE） - 知乎 (zhihu.com)

【2023Q2】LLM炼丹trick拾遗：LLM的MoE架构与Lifelong learning - 知乎 (zhihu.com)